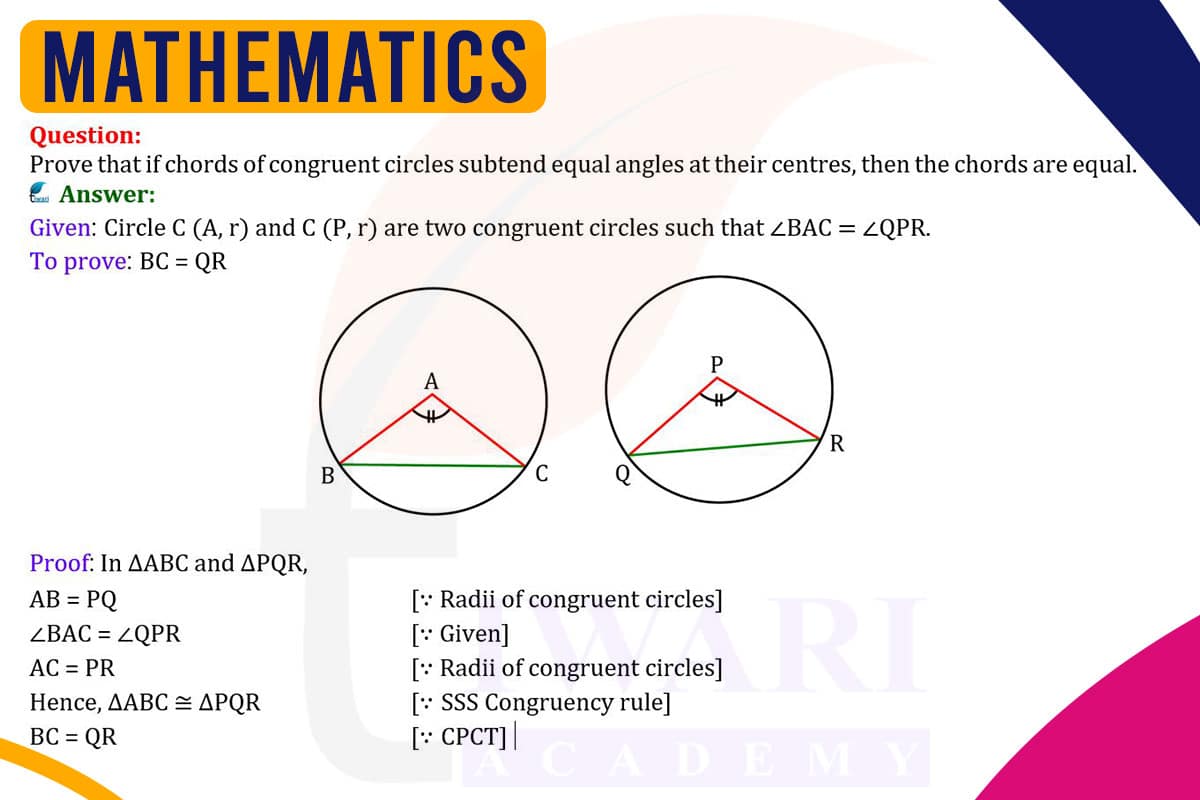
To prove that if chords of congruent circles subtend equal angles at their centers, then the chords are equal, consider two congruent circles with chords subtending equal angles at the centers. Since the circles are congruent, they have equal radii. The equal subtended angles imply that the isosceles triangles, formed by the radii and the chords, are congruent (by the Angle-Side-Angle postulate, as the angles at the center and the radii are equal). Since corresponding parts of congruent triangles are equal, the chords, which are corresponding parts, must be equal. Thus, if chords in congruent circles subtend equal angles, the chords themselves are equal.
Let’s discuss in detail
Chords and Congruent Circles
In the realm of geometry, congruent circles and chords play a pivotal role in understanding spatial relationships. Congruent circles are circles with the same radius, and a chord is a line segment with both endpoints on the circle. The study of chords in congruent circles becomes intriguing when we explore the angles they subtend at the center. A key question arises: if chords in congruent circles subtend equal angles at their centers, are the chords themselves equal? This question leads us into a deeper exploration of geometric principles and their implications.
Equal Angles in Congruent Circles
The premise of our exploration is based on two congruent circles, each with a chord that subtends an equal angle at the circle’s center. The congruence of the circles ensures that they have identical radii, a fact that is crucial for our proof. The equal angles subtended by the chords suggest a symmetry that might extend to the chords themselves. This symmetry is not immediately apparent but can be deduced through geometric reasoning, specifically by examining the properties of the triangles formed by the chords and the radii.
Isosceles Triangles and Their Properties
In each circle, the chord and the two radii to its endpoints form an isosceles triangle. The two radii are equal by the definition of a circle, making the triangle isosceles. In an isosceles triangle, the angles opposite the equal sides (the radii) are also equal. These angles are key to our proof, as they are the angles subtended by the chords. The equality of these angles in both circles is the starting point for proving the equality of the chords.
Congruence of Triangles
The equal angles subtended by the chords, along with the equal radii of the congruent circles, imply that the isosceles triangles in each circle are congruent to each other. This congruence is established by the Angle-Side-Angle (ASA) postulate, which states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent. In our case, the equal angles at the center and the equal radii (sides) fulfill these conditions.
Deduction of Equal Chords
From the congruence of the isosceles triangles, it follows that all corresponding parts of these triangles are equal. This includes the chords, which are the bases of the isosceles triangles. Therefore, the equality of the angles subtended by the chords leads to the conclusion that the chords themselves must be equal. This conclusion is a direct result of the properties of congruent triangles and the specific geometric configuration of our congruent circles and their chords.
Symmetry and Equality in Geometry
In conclusion, the exploration into chords of congruent circles subtending equal angles reveals a fundamental geometric principle: the symmetry in angles leads to symmetry in line segments. This proof not only underscores the elegance of geometric relationships but also highlights the interconnectedness of various geometric elements. Understanding such relationships is crucial in the broader context of geometric studies and their practical applications in fields ranging from design to physics.
Discuss this question in detail or visit to Class 9 Maths Chapter 9 for all questions.
Questions of 9th Maths Exercise 9.1 in Detail

