NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.1 Circles in PDF file format to download for offline use. Class 9 Maths Exercise 9.1 is solve here in Hindi and English Medium based on revised syllabus and following new books for CBSE 2025-26 and State boards students.
Class 9 Maths Exercise 9.1 Questions in Detail

| Class: 9 | Mathematics |
| Chapter: 9 | Exercise: 9.1 |
| Topic Name: | Circles |
| Content Type: | Text, PDF and Videos |
| Session: | CBSE 2025-26 |
| Medium: | English and Hindi Medium |
Terms of Circle – Radius and Chord
If two points on the circumference of the circle are joined by a line segment, it is known as Chord. There can be infinite numbers of chord which can be drawn in a circle. The Chord passing through the center of a circle is called diameter of the Circle.
In spoken language, we use the term Dia instead of speaking the full word diameter. The diameter of a circle is double the radius. The Radius is a line segment joining the center of a circle to its circumference. Just like a chord there can be infinite number of diameters and Radii. By using the formula of circumference of a circle and area of circle many question can be solved.
Parts of Circle – Major and Minor arc
A piece of a circle or a part of a circle between any two points is called as an Arc. So, a circle can be split in to two parts. In terms of a minor arc and a major arc. The length of the complete circle is called its circumference. The circumference of a circle varies directly with radius of the circle.
Segments of a Circles
The region between a chord and any of its Arcs is known a segments. So, in any circle we shall have a minor segment a major segment. We also come across another term called Sector. This is region between an arc of a circle and two Radii. Just as we have a major segment and minor segment, we have a minor sector and major sector also.
Important Questions of 9th Maths Exercise 9.1
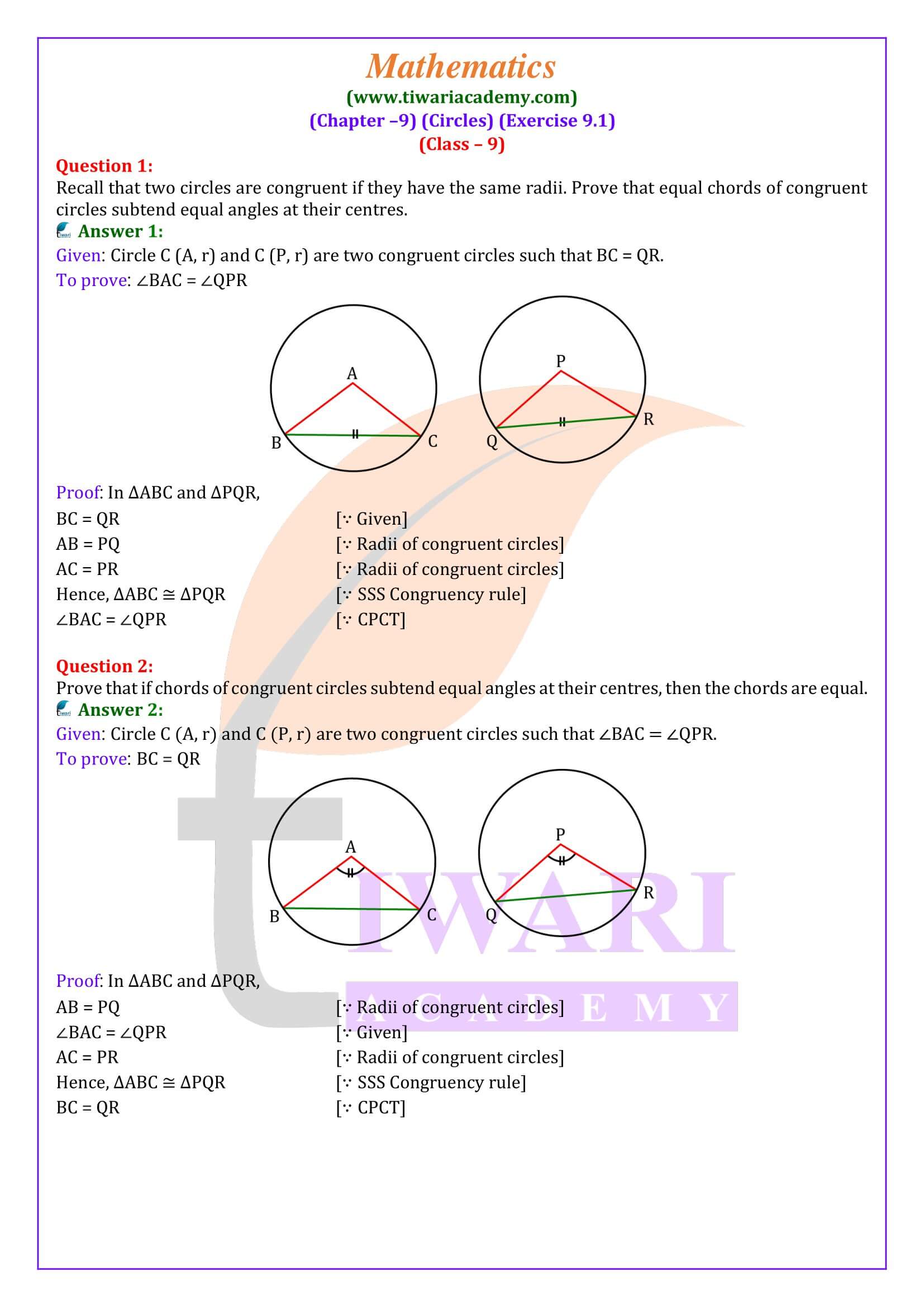
Exercise 9.1 consist of two theorems only and both are equally important. The first one is that equal chords of a circle subtend equal angles at the center.
The second one is the converse of the theorem and says that if the angles subtended by chord of the circle at the center of the circle then the chords must be equal.