NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.2 Heron’s Formula in Hindi and English medium updated for CBSE and State Boards. Dive into Class 9 Maths with Tiwari Academy’s updated NCERT solutions for Chapter 12, Exercise 12.2 on Heron’s Formula. Available in Hindi and English for all boards, our concise guides help you master the concepts quickly and efficiently. Get ready to excel with our expert resources!
NCERT Solutions for Class 9 Maths Exercise 12.2
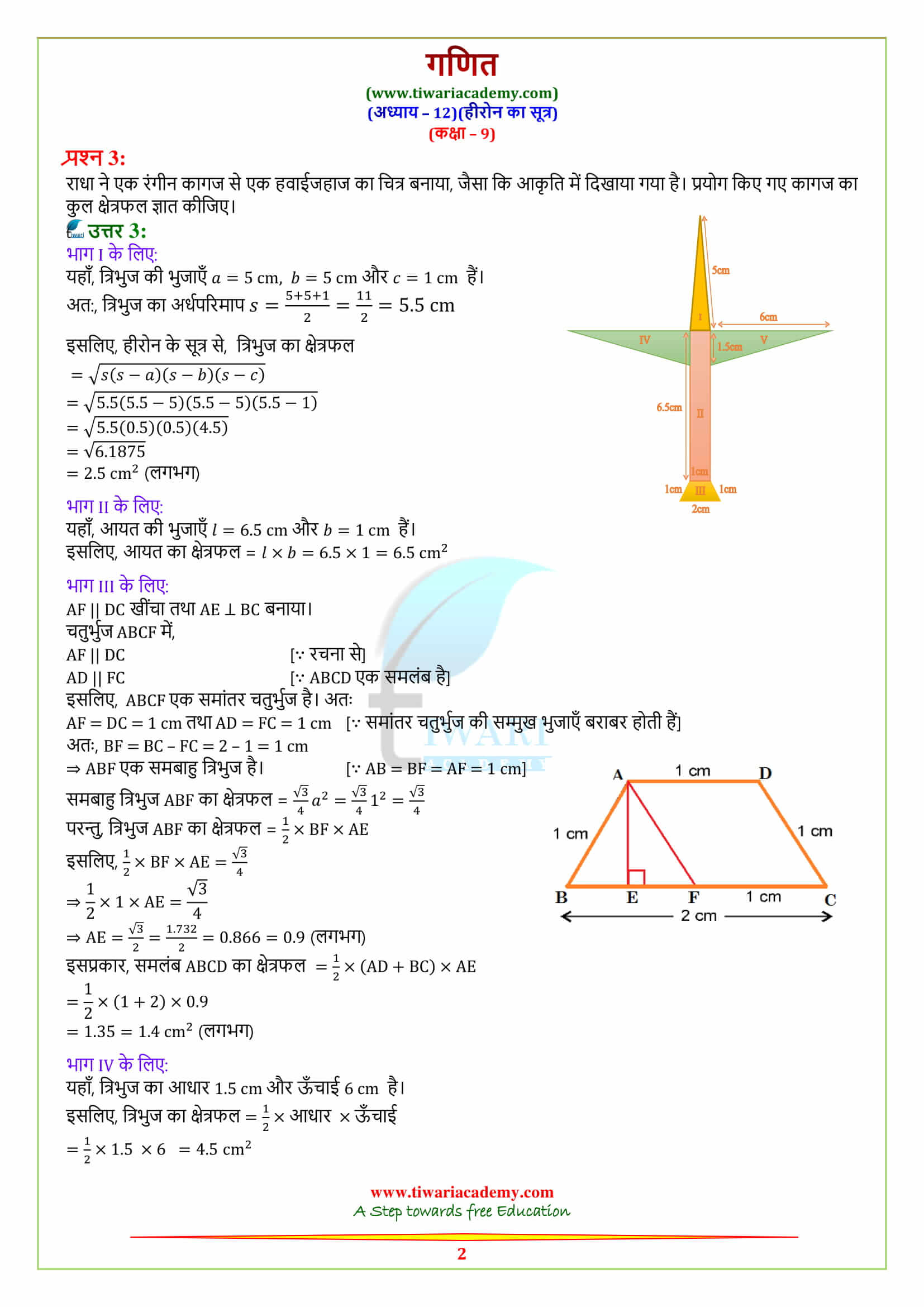
Exercise 12.2 of Class 9 Maths contains 9 questions in all. Most of the questions are easy to understand and solve. A few students find question number 9 as difficult to solve. Get here complete explanation through video and text solutions.
Contribution of Mathematicians
Till now you have studied a lot of Greek mathematicians and their important contributions but for us, in India, there is Bhaskara II. He was an Indian mathematician and astronomer who contributed to arithmetic, algebra, and mathematics of planets.
He also discovered the principles of calculus. In the second part of chapter 12 from NCERT solutions for Maths class 9, you will learn how you can use the Heron formula for quadrilaterals.
| Class: 9 | Mathematics |
| Chapter: 12 | Exercise 12.2 |
| Content: | NCERT Exercise Solutions |
| Mode: | Online Text and Videos Format |
| Medium: | Hindi and English Medium |
Applications and proof of Heron’s formula
With the help of explanation 12.2 and examples 5 and 6, you calculated the area of a quadrilateral. If all the sides and diagonals are givens, find the area by simply dividing the quadrilateral into equal parts. The above said can be later proven with the help of two methods – (a) Pythagoras Theorem, (b) Trigonometric Identities.
About Exercise 12.2 Class 9 Maths
In class 9 Maths Exercise 12.2, most of the questions are based on multiple figures. For example – group of triangles and rectangles, or multiple triangles. For the simplicity, we can apply Pythagoras theorem in case of right angle triangles.
However, there are only a few following applications of heron’s formula: (a) Used for calculating the area of a triangle, if the length of sides of a triangle is mentioned and (b) Used for calculating the area of a quadrilateral, if the values of sides and one diagonal is given.
Solving Exercise 12.2 using Heron’s Formula
Once you complete exercise 12.2, all 9 questions, you finally complete the chapter 12. This shall prove that you have understood the concepts of Heron’s Formula. However, a summary of the chapter is given at the end of the page which consists of two fundamental knowledge. You will use these during the solutions of exercise 12.2.
There are certain things that we suggest you to keep in mind (a) There are three different types of triangles, formally known as Equilateral, isosceles, and scalene. But Pythagoras worked for the right-angled triangles only. (b) Before using the heron formula for calculating the quadrilateral you have to divide it into triangles. (c) Heron’s formula can be used to find area of all types of triangles.
Which is the most important question of class 9 Maths exercise 12.2?
There are total 9 questions in Exercise 12.2 of class 9th Maths. Out of these question number 9 is one of the most important question for a student in grade IX. This question is little bit tricky and need some construction to find out the height of rhombus.
How many questions are there in exercise 12.2 of 9th Mathematics?
There are all together nine questions in ex. 12.2. Most of the questions are combination of two figures. The two figures may be two triangles or one triangle with quadrilateral.
What are the application of exercise 12.2 of Heron’s Formula for class 9?
As we know that Heron’s Formula is a mathematical expression used to calculate the area of all type of triangle, if the lengths of all three sides are known. In class 9, it can be used to solve simple problems in mensuration, including finding the area of a quadrilateral or any polygon dividing it into triangles. It can also be used to calculate the area of any triangle in real-life situations.