NCERT Solutions for Class 8 Maths Chapter 4 Exercise 4.1 Practical Geometry in Hindi and English medium updated for CBSE and State Boards. Access Tiwari Academy’s updated NCERT Class 8 Maths solutions for Chapter 4 Exercise 4.1 on Practical Geometry. Available for free in both Hindi and English, these resources are perfect for CBSE and State Board students seeking a clear understanding of geometry concepts.
8th Maths Exercise 4.1 Solution in Hindi and English Medium
Class 8 Maths Chapter 4 Exercise 4.1 Solution
Class VIII Mathematics Ex. 4.1 of Practical Geometry in PDF file format updated for academic session 2025-26 free to use online or download for offline. All the solutions are in text, PDF, as well as videos format free to use without any per-registration. Class 8 NCERT Book Maths Exercise 4.1 deals with the construction of quadrilateral when all four sides and a diagonal is given.
| Class: 8 | Mathematics |
| Chapter: 4 | Exercise: 4.1 |
| Chapter Name: | Practical Geometry |
| Medium: | English and Hindi |
| Content Mode: | Online and Offline |
When four sides and one diagonal are given.
Construct a quadrilateral ABCD in which AB = 4.8 cm, BC = 4.3 cm, CD = 3.6 cm, AD = 4.2 cm and diagonal AC = 6 cm.
First we draw a rough sketch of quad.
ABCD and write down its dimension,
We may divide it into triangles, namely Triangle ABC and Triangle ACD.
Steps of construction
Step 1. Draw AB = 4.8 cm.
Step 2. With A as centre and radius equal to 6 cm, drew an arc.
Step 3. With B as centre and radius equal to 4.3 cm, draw another arc, cutting the previous arc at C.
Step 4. Join BC.
Step 5. With A as centre and radius equal to 4.2 cm draw an arc.
Step 6. With C as centre and radius equal to 3.6 cm, draw another arc, cutting the previous arc at D.
Step 7. Join AD and CD. Then, ABCD is the required quadrilateral.
Construct a quadrilateral ABCD in which AB = 4.2 cm, BC = 6 cm, CD = 5.2 cm, DA = 5 cm and AC = 8 cm.
Steps of construction
Step 1. Draw AB = 4.2 cm.
Step 2. With A as centre and radius equal to 8 cm, drew an arc.
Step 3. With B as centre and radius equal to 6 cm, draw another arc, cutting the previous arc at C.
Step 4. Join BC.
Step 5. With A as centre and radius equal to 5 cm draw an arc.
Step 6. With C as centre and radius equal to 5.2 cm, draw another arc, cutting the previous arc at D.
Step 7. Join AD and CD. Then, ABCD is the required quadrilateral.
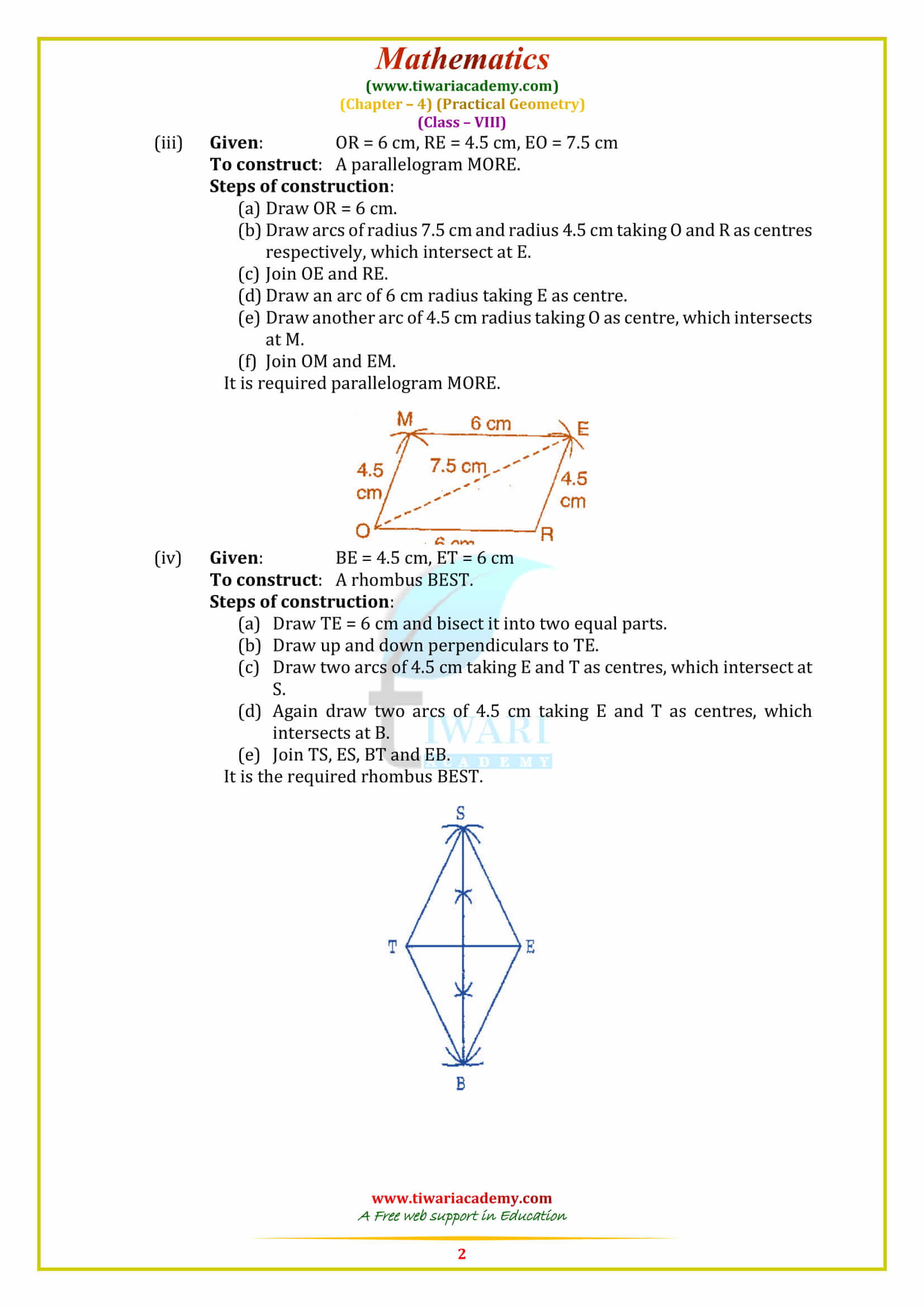
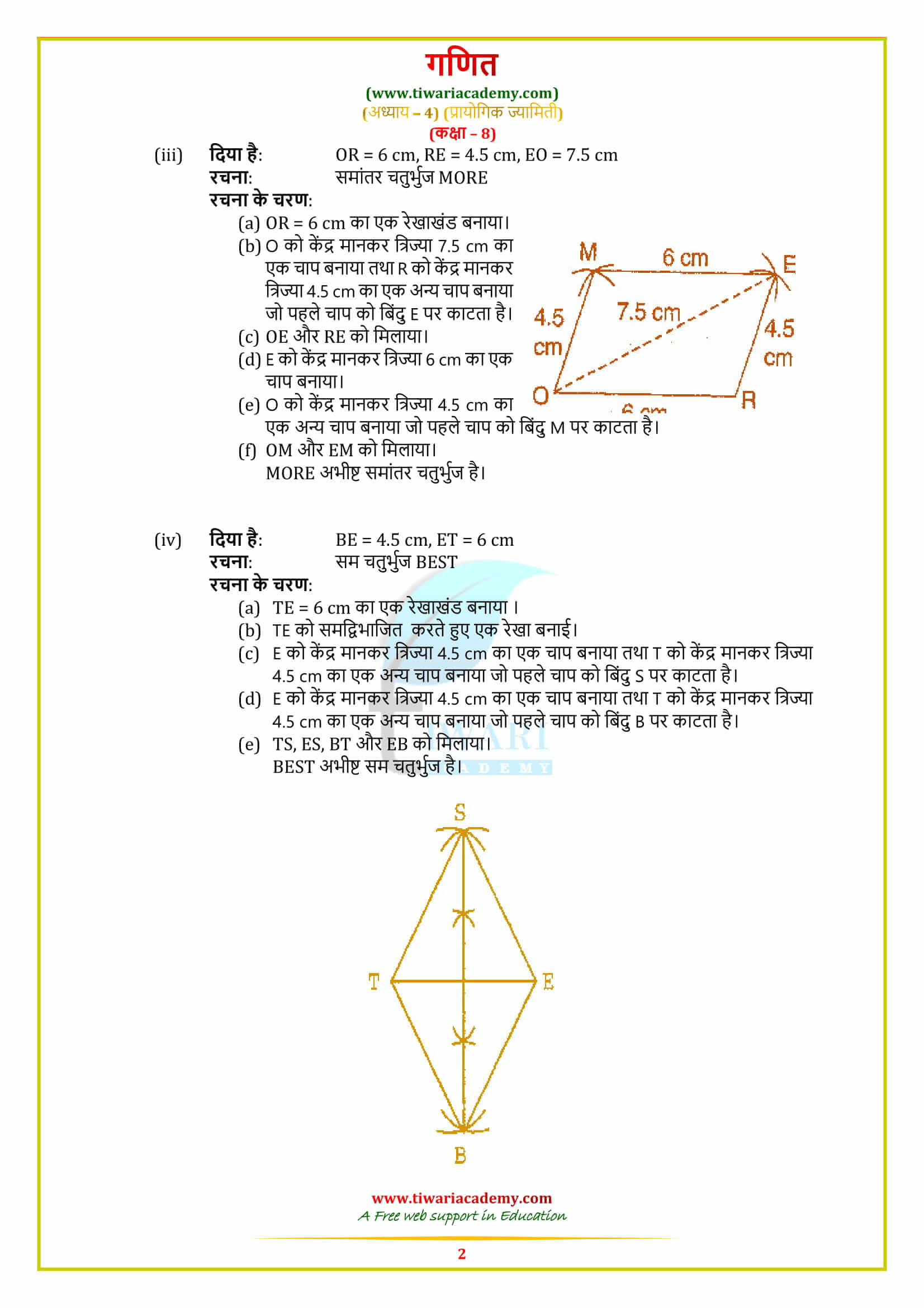
Construction of Quadrilaterals
We know that a quadrilateral has ten parts in all: four sides, four angles and two diagonals. To construct a quadrilateral, we shall need data about five specified parts of it. We consider the following five cases and illustrate the construction in each case by an example. We divide the required quadrilateral into two triangles which can be easily constructed. These two triangles together will form a quadrilateral.
Class 8 Maths Exercise 4.1 Extra Questions for Practice
How many parts are required to construct a quadrilateral?
To construct a quadrilateral, we required five parts.
We know that a quadrilateral has ten parts in all: four sides, four angles and two diagonals. To construct a quadrilateral, we shall need data about five specified parts of it.
What is the appropriate condition to construct a quadrilateral?
A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal are given. A quadrilateral can be constructed uniquely if the lengths of its three sides and two diagonals are given. A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are given.
Is it possible to draw a quadrilateral whose all angles are obtuse angles?
No, all the four angles of a quadrilateral cannot be obtuse.
A quadrilateral refers to a polygon that has four sides. A quadrilateral has more properties linked with it than a triangle. Moreover, a quadrilateral can have parallel opposite sides. Therefore, if every side holds a parallel opposite side it is a parallelogram.
To construct a unique quadrilateral given the following measurements:
- (i) When four sides and one diagonal are given.
- (ii) When two diagonals and three sides are given.
- (iii) When two adjacent sides and three angles are given.
- (iv) When three sides and two included angles are given.
- (v) When other special properties are known.