NCERT Solutions for Class 7 Maths Chapter 8 Exercise 8.2 Rational Numbers in Hindi and English with videos solution for CBSE 2025-26 exams. Questions of ex. 8.2 class 7th mathematics are revised according to new syllabus and latest textbooks for academic session 2025-26.
NCERT Class 7 Maths Exercise 8.2 Solution in Hindi and English Medium
| Class: 7 | Mathematics |
| Chapter: 8 | Exercise: 8.2 |
| Chapter Name: | Rational Numbers |
| Content Type: | PDF and Videos Format |
| Session: | CBSE 2025-26 |
| Medium: | Hindi and English Medium |
Class 7 Maths Chapter 8 Exercise 8.2 Solution
All the contents are updated as per the latest CBSE Syllabus 2025-26 CBSE and state board students. In NCERT book exercise 8.2 of class vii math, we will practice the questions based on the concept of addition and subtraction of rational numbers taking LCM. Students need little bit more time to practice and become confident in this topic.
Class 7 Maths Chapter 8 Exercise 8.2 Solution in Videos
Comparison of Rational Numbers
It is clear that:
(i) every positive rational number is greater than 0.
(ii) every negative rational number is less than 0.
Compare Two Rational Numbers
Step 1. Express each of the two given rational numbers with positive denominator.
Step 2. Take the LCM of these positive denominators.
Step 3. Express each rational number (obtained in Step 1), with this LCM as the common denominator. Step 4. The number having the greater numerator is greater.
Three Important Properties of Rational Numbers
Property 1:
For each rational number x, exactly one of the following is true:
(i) x > 0 (ii) x = 0 (iii) x < 0
Property 2:
For any two rational numbers x and y. exactly one of the following is true:
(i) x > y (ii) x = y (iii) x < y
Property 3:
If x, y and < be rational numbers such that x > y and y > z then x > z.
Addition of Rational Numbers
Suppose we have to add two given rational numbers. First convert each of them into a rational number with a positive denominator.
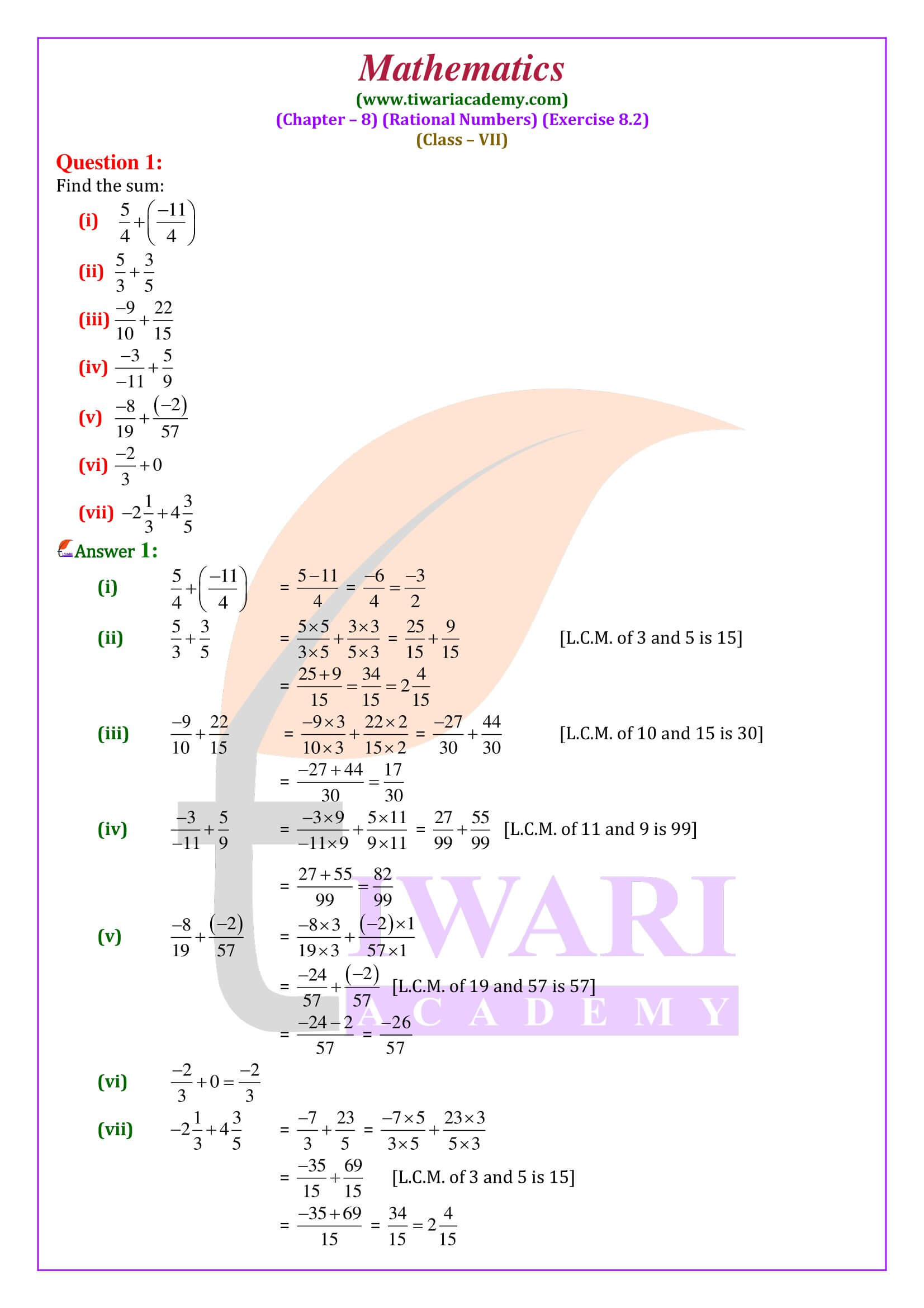
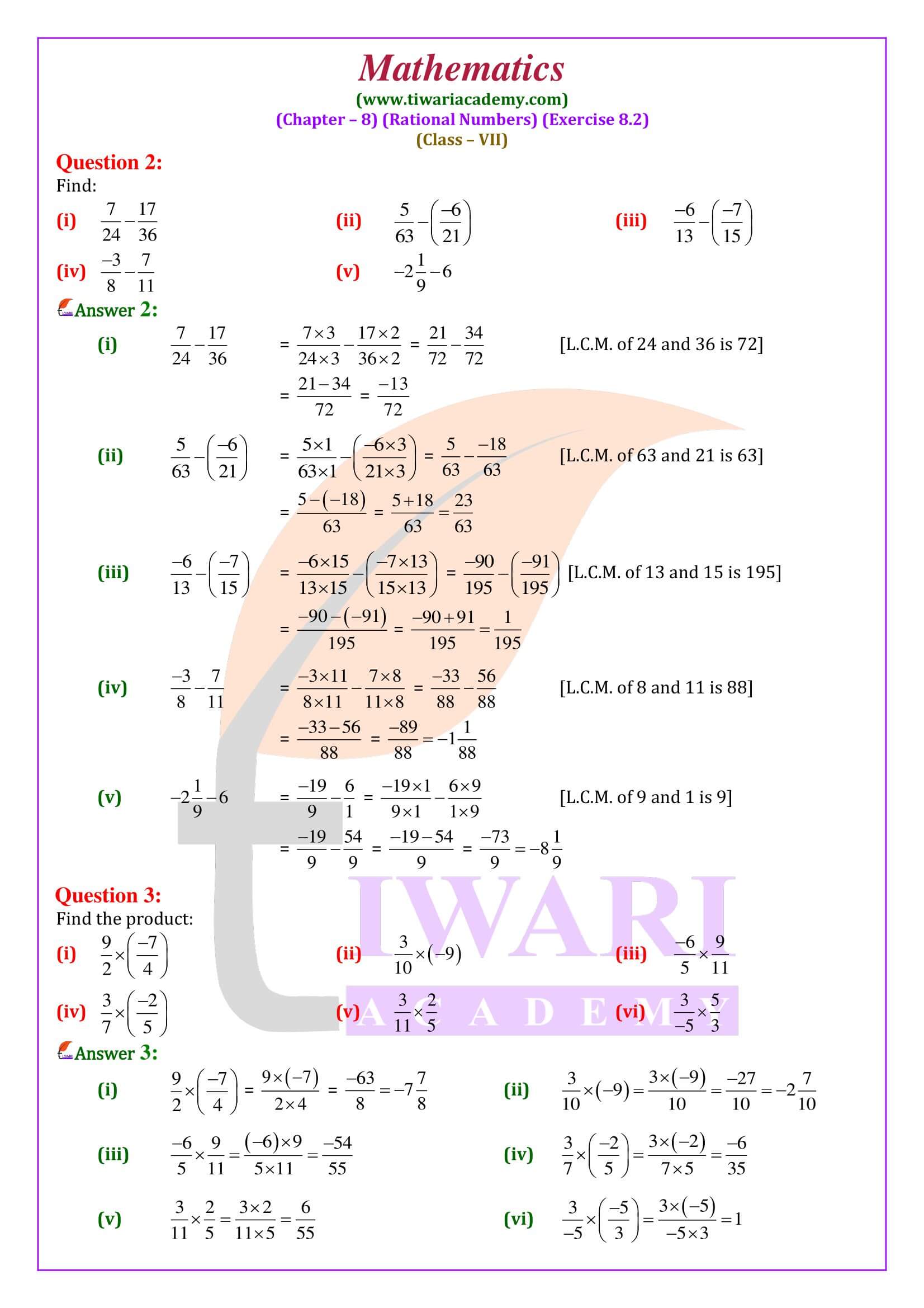
Class 7 Maths Exercise 8.2 Extra Questions
Add 5/9 and -13/9.
We have:
5/9 + (-13)/9 = (5 – 13)/9 = -8/9
CASE-2: When Denominators of Given Numbers are Unequal:
Step 1. Take the LCM of the denominators of the given rational numbers.
Step 2. Express each of the given rational numbers with the above LCM as the common denominator. Step 3. Now, add the numbers as shown in Case I.
Add -2/3 and 3/4.
The denominators of the given rational numbers are 3 and 4. LCM of 3 and 4 is 12.
-2/3 = {(-2) x 4}/ (3 x 4) = -8/12
And ¾ = (3 x 3)/ (4 x 3) = 9/12
Now, -8/12 + 9/12 = 1/12
Subtract ¾ from 2/3
We have:
2/3 – ¾ = 2/3 + (additive inverse of ¾)
2/3 + -3/4 = (8 -9)/12 = -1/12
CASE 1: When Denominators of Given Numbers are Equal.
Let p/q and r/q be any two rational numbers.
Then, we define (p/q + r/q) = (p + q)/q
Thus, in order to add two rational numbers with the same denominator, we simply add their numerators and divide the sum by the common denominator.
Subtraction of Rational Numbers
For any two rational numbers a/b and c/d, we define:
a/b – c/d = a/b + (-c/d)
We say that the additive inverse of c/d
a/b – c/d = a/b + additive inverse of c/d
hence, a/b – (-c/d) = a/b + c/d
Class 7 Maths Exercise 8.2 Important Questions
What are the four operations when working with rational numbers?
There are four basic arithmetic operations with rational numbers: addition, subtraction, multiplication, and division.
How do you simplify rational numbers?
Step 1: Factor the numerator and the denominator.
Step 2: List restricted values.
Step 3: Cancel common factors.
Step 4: Simplify and note any restricted values not implied by the expression.
Why is division not closed for rational numbers?
The rationals are not closed under division because of the possibility of division by zero. Zero is a rational number and division by zero is undefined.
Multiplication of Rational Numbers
The product of two rational numbers is defined below:
Product of two rational numbers = Product of their numerators/ Product of their denominators
Thus, for any rational number a/b and c/d we have:
(a/b x c/d) = (a x c)/ (b x d)
Find the product: 2/3 x 5/7
We have:
2/3 x 5/7 = (2 x 5)/ (3 x 7) = 10/ 21
Reciprocal or Multiplicative Inverse of a Rational Number
If the product of two rational numbers is 1 then each one is called the reciprocal of the other.
Thus, the reciprocal of is a/b and b/a we write. a/b = b/a
Clearly, (i) reciprocal of 0 does not exist.
(ii) reciprocal of 1 is 1.
(iii) Reciprocal of -1 is -1.
Division of Rational Numbers
If a/b and c/d are two rational numbers such that c/d ≠ 0, then we define:
(a/b)/ (c/d) = a/b x d/c