NCERT Solutions for Class 6 Maths Chapter 1 Exercise 1.1 in Hindi and English Medium modified and updated for CBSE 2025-26 session. Get here the revised solutions of 6th Maths ex. 1.1 prepared according to new syllabus and latest NCERT Books for CBSE 2025-26.
6th Maths Exercise 1.1 Solutions in Hindi and English Medium
Class 6 Maths Chapter 1 Exercise 1.1 Solutions
Class VI Mathematics NCERT Book Ex. 1.1 of chapter 1 Knowing Our Numbers in PDF file format free to use in Hindi Medium as well as English Medium. Additional questions with answers are also given for practice. All the contents are updated for CBSE session 2025-26 for state board students also. Videos solutions are also available to use online free or download.
| Class: 6 | Mathematics |
| Chapter: 1 | Exercise: 1.1 |
| Topic Name: | Knowing Our Numbers |
| Content: | NCERT Solutions and Notes |
| Session: | CBSE 2025-26 |
| Medium: | Hindi and English Medium |
More about Class 6 Maths Exercise 1.1
In earlier classes, we have studied numbers, small as well as large. We have studied the four basic operations on these numbers. We have studied about patterns in number sequences and done many other interesting things with the numbers. In this chapter, we shall study such interesting things with a bit of review and revision as well.
Know about Natural Numbers
We use numbers 1, 2, 3, 4 … to count and calculate. Therefore, these numbers are called Counting Numbers. However, we also use the name natural numbers for counting numbers. Thus, 1, 2, 3…, 10…, 80… 1005 … are all natural numbers.
Since we start counting with the number 1, therefore, 1 is the first or the smallest natural number. The next number is 2 which is obtained by adding 1 to the first natural number. By adding 1 to 2, we get 3, the third natural number. In fact, by adding 1 to a natural number, we get the next natural number. Thus, 30 (= 29 + 1) is the natural number next to 29.
What are Whole Numbers?
In order to describe the number of elements in a collection with no objects, we use the symbol ‘0’ called zero. The number ‘0’ together with the natural numbers gives us the numbers 0, 1, 2, 3, 4 … which are called whole numbers.
- Digits: In order to represent any number, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These ten symbols are called digits or figures.
- Numeral: A group of digits denoting a number is called a numeral.
For example, 5467, 20346, 945860 etc. are numerals. - Notation: The method of representing a number in digits or figures is called notation.
- Numeration: The method of expressing a number in words is called numeration.
Methods of Numeration
There are two commonly used methods of numeration:
(i). Indian System of Numeration
(ii). International System of Numeration
In Indian system, a number is split up into groups or periods starting from the right. The groups are called ones, thousands, lakhs, crores and arabs. The ones in turn are split into hundreds, tens and units.
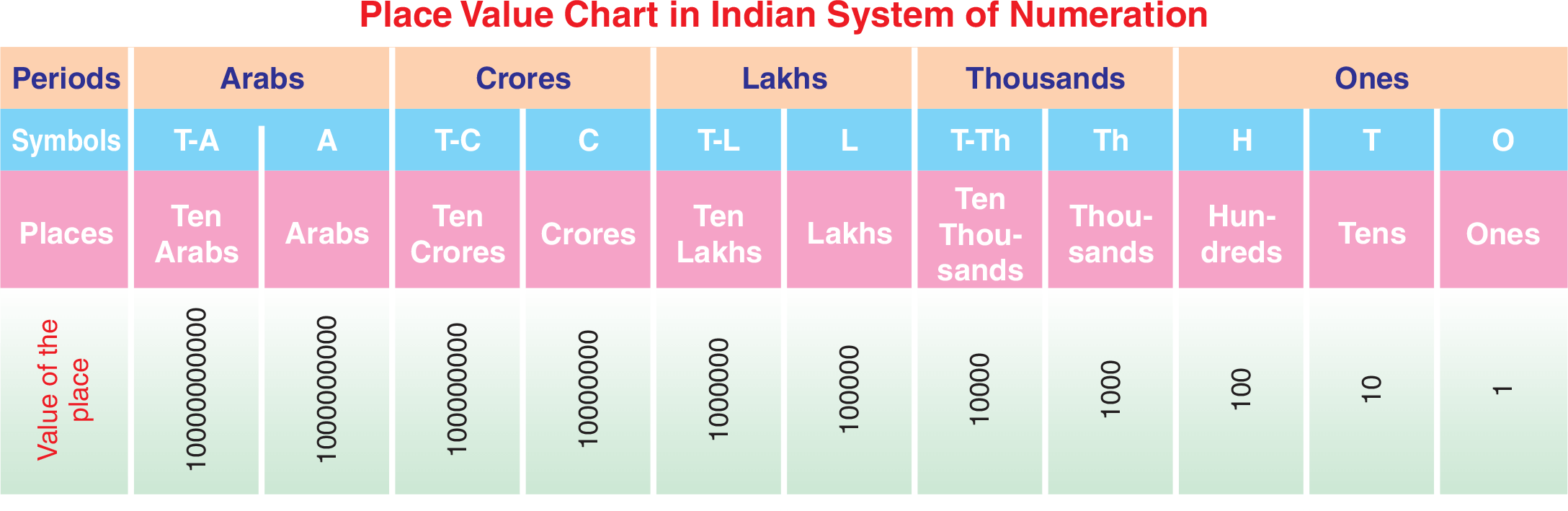
Generally, we separate the periods by marking commas (,). In the modern notation, we leave a short space between the periods, instead of using a comma. Thus, 468572309 is written as 46,85,72,309 or 46 85 72 309. It is read as forty-six crore eighty-five lakh seventy-two thousand three hundred nine.
This number represents a collection of 46 crores, 85 lakhs, 72 thousands, 3 hundreds and 9 ones. Therefore, we can write it in expanded form as under: 46,85,72,309 = 4 × 100000000 + 6 × 10000000 + 8 × 1000000 + 5 × 100000 + 7 × 10000 + 2 × 1000 + 3 × 100 + 0 × 10 + 9 × 1.
Important Questions on Class 6 Maths Exercise 1.1
How many natural numbers can be there?
If we start counting 1, 2, 3… 8, 9… 100… 190, 191… 300 … and continue to count, there would be no end. Even if we continue to count day and night for our whole life; still we cannot reach end. In other words, we cannot complete the counting of natural numbers. Obviously, there is no last or the greatest natural number.
What is the difference of the place values of two 5’s in 86542359?
The 5 in the second place from the right is at ten’s place.
So, place value of 5 in ten’s place = 50.
The second 5 is in the 6th place from the right.
So, it is at lakh’s place.
So, Place value of other 5 = 500000.
Hence, required difference = 500000 – 50 = 499950.
How many 6-digit numbers are there in all?
The largest 6-digit number = 999999
The smallest 6-digit numbers = 100000
Number of all 6-digit numbers = (999999 – 100000) + 1
= 899999 + 1 = 900000.
Hence, the number of all 6-digit numbers is nine lakhs.
International System of Numeration
The International System of Numeration is being followed by most of the countries of the world. In this
system also, a number is split up into groups or periods. Starting from the right, the groups are called
ones, thousands, millions and billions. The ones in turn are split into hundreds, tens and ones.

How many problems are there in exercise 1.1 of class 6th Maths Chapter 1?
There are 4 problems in exercise 1.1 of class 6th Maths Chapter 1 (Knowing our Numbers). Question 1 having 5 parts, question 2 with five parts, question 3 having four parts, question 4 with four parts. All parts of all questions are easy, good, and important.
What type of questions can come from exercise 1.1 of class 6th Maths in the school exams?
Exercise 1.1 of class 6th Maths contains straightforward and nice questions. Most probably, fill in the blanks, true or false (yes or no), one-word answer, MCQ type questions can come from exercise 1.1 of class 6th Maths in the school exams.
Can students prepare exercise 1.1 of class 6th Maths in 2-3 hours?
Students can prepare exercise 1.1 of class 6th Maths in 2-3 hours or not depends on student’s working speed, efficiency, capability, and many other factors. But if they try to prepare exercise 1.1 of class 6th Maths in 2-3 hours, they can do that because exercise 1.1 is very short and easy.
What is the international system of numeration in exercise 1.1 of 6th class Maths?
In the International System of Numeration, as it is being used we have ones, tens, hundreds, thousands, and then millions. One million is a thousand thousands. Commas are used to mark thousands and millions. It comes after every three digits from the right to left. The first comma marks thousands, and the next comma marks millions. For example, the number 60,801,592 is read in the International System as sixty million eight hundred one thousand five hundred ninety-two. In the Indian System, it is six crore eight lakh one thousand five hundred ninety-two.





