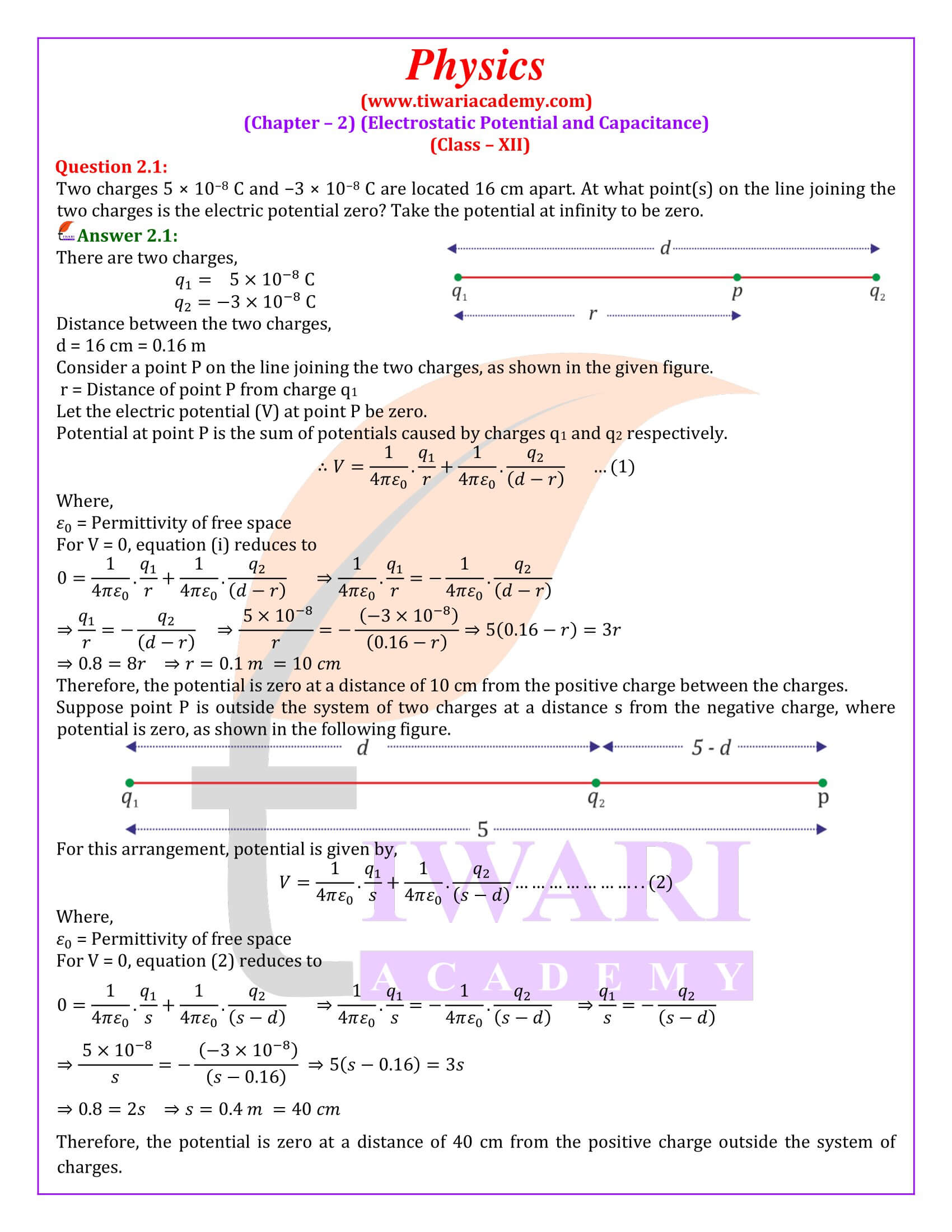
NCERT Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Exercises and Additional Exercises in Hindi and English Medium PDF free download updated for 2025-26. The additional exercises are not in syllabus as per the new NCERT textbooks issued for academic session 2025-26.
Practical Viva for Class 12 Physics
How to Prepare for Class 12 Physics Exam
Study Guide for Class 12 CBSE Board 2025
NCERT Solutions for Class 12 Physics Chapter 2
Chapter 2 Electrostatic Potential and Capacitance Solutions
- Class 12 Physics Chapter 2 Exercises Solutions
- 12th Physics Chapter 2 Additional Exercises (Not in Syllabus)
- Class 12 Physics Chapter 2 Solutions in Hindi
- Class 12 Physics NCERT Book Chapter 2
- Class 12 Physics Revision Book Chapter 2
- Revision Book Answers
- Class 12 Physics Chapter 2 Revision Notes 1
- Class 12 Physics Chapter 2 Revision Notes 2
- Class 12 Physics Chapter 2 Quick Revision
- Class 12 Physics Chapter 2 Revision Questions
- Visit to 12th Physics Main Page

Download UP Board Solutions, NCERT Solutions and NCERT Apps based on updated CBSE Syllabus 2025-26. If you have any doubt, please visit to discussion forum to ask your doubts.
| Class: 12 | Physics |
| Chapter 2: | Electrostatic Potential and Capacitance |
| Content: | Exercises Question Answers and Notes |
| Content Mode: | PDF, Videos and Text Format |
| Academic Year: | Session 2025-26 |
| Medium: | Hindi and English |
Class 12 Physics Chapter 2 Solutions in English
NCERT Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance exercises are given below to use it online or download in PDF form for offline. Ask your doubts related to NIOS or CBSE Board or any other educational fact through Discussion Forum and reply to the other users. Download NCERT Books 2025-26 based on latest CBSE Syllabus for all boards who are following CBSE.

Questions from Board Papers
1. What is the ratio of electric field intensity at a point on the equatorial line to the field at a point on axial line when the points are at the same distance from the centre of the dipole?
2. For an isolated parallel plate capacitor of capacitance C and potential difference V, what will happen to (i) charge on the plates (ii) potential difference across the plates (iii) field between the plates (iv) energy stored in the capacitor, when the distance between the plates is increased? [Answer: (i) No change (ii) increases (iii) No change (iv) increases].
3. A storage capacitor on a RAM (Random Access Memory) chip has a capacity of 55pF. If the capacitor is charged to 5.3V, how may excess electrons are on its negative plate?[Answer: 1.8 × 10^9]
4. The potential at a point A is –500V and that at another point B is +500V. What is the work done by external agent to take 2 units (S.I.) of negative charge from B to A.
5. In charging a capacitor of capacitance C by a source of emf V, energy supplied by the sources QV and the energy stored in the capacitor is ½QV. Justify the difference.
Important Questions for practice
1. A point charge Q is kept at the intersection of (i) face diagonals (ii) diagonals of a cube of side a. What is the electric flux linked with the cube in (i) & (ii)?
2. Using Gauss’s theorem in electrostatics, deduce an expression for electric field intensity due to a charged spherical shell at a point (i) inside (ii) on its surface (iii) outside it. Graphically show the variation of electric field intensity with distance from the centre of shell.
3. A conducting slab of thickness ‘t’ is introduced between the plates of a parallel plate capacitor, separated by a distance d (t is less than d). Derive an expression for the capacitance of the capacitor. What will be its capacitance when t is equal to d?
4. A potential difference V is applied across a conductor of length L and diameter D. How are the electric field E and the resistance R of the conductor affected when (i) V is halved (ii) L is halved (iii) D is doubled.
Justify your answer.
5. What is an equipotential surface? Write three properties Sketch equipotential surfaces of (i) Isolated point charge (ii) Uniform electric field (iii) Dipole
Important Questions on 12th Physics Chapter 2
A spherical conductor of radius 12 cm has a charge of 1.6 × 10⁻⁷C distributed uniformly on its surface. What is the electric field inside the sphere?
Radius of the spherical conductor, r = 12 cm = 0.12 m Charge is uniformly distributed over the conductor, q = 1.6 × 10⁻⁷ C Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.
Three capacitors of capacitances 2pF, 3pF and 4pF are connected in parallel. What is the total capacitance of the combination?
Capacitances of the given capacitors: C₁ = 2 pF, C₂ = 3 pF and C₃ = 4 pF For the parallel combination of the capacitors, equivalent capacitor is given by Ceq the algebraic sum, Therefore Ceq = C₁ + C₂ + C₃ = 2 + 3 + 4 = 9 pF Therefore, total capacitance of the combination is 9 pF.
Explain what would happen if in the capacitor given in Exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates, While the voltage supply remained connected.
Dielectric constant of the mica sheet, k = 6 If voltage supply remained connected, voltage between two plates will be constant. Supply voltage, V = 100 V Initial capacitance, C = 1.771 × 10⁻¹¹ F New capacitance, C₁ = kC = 6 × 1.771 × 10⁻¹¹ F = 10⁶ pF New charge, q₁ = C₁V = 10⁶ × 100 pC = 1.06 × 10⁻⁸ C Potential across the plates remains 100 V.
Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.
Yes The electric field intensity inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop is zero because the field inside the conductor is zero. Hence, electric field is zero, whatever is the shape.
Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.
When a charged particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of electrostatic field is continuous from one side of a charged surface to the other.
Two large conducting spheres carrying charges Q₁ and Q₂ are brought close to each other. Is the magnitude of electrostatic force between them exactly given by Q₁Q₂/4πϵ₀ r², where r is the distance between their centres?
The force between two conducting spheres is not exactly given by the expression, Q₁ Q₂/4πϵ₀r², because there is a non-uniform charge distribution on the spheres.
If Coulomb’s law involved 1/r³ dependence (instead of 1/r²), would Gauss’s law be still true?
Gauss’s law will not be true, if Coulomb’s law involved 1/r³ dependence, instead of1/r², on r.
A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
Yes, If a small test charge is released at rest at a point in an electrostatic field configuration, then it will travel along the field lines passing through the point, only if the field lines are straight. This is because the field lines give the direction of acceleration and not of velocity.
What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
Whenever the electron completes an orbit, either circular or elliptical, the work done by the field of a nucleus is zero.
We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
No Electric field is discontinuous across the surface of a charged conductor. However, electric potential is continuous.
What meaning would you give to the capacitance of a single conductor?
The capacitance of a single conductor is considered as a parallel plate capacitor with one of its two plates at infinity.
Guess a possible reason why water has a much greater dielectric constant (80) than say, mica (6).
Water has an unsymmetrical space as compared to mica. Since it has a permanent dipole moment, it has a greater dielectric constant than mica.
The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm⁻¹. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside!)
We do not get an electric shock as we step out of our house because the original equipotential surfaces of open air changes, keeping our body and the ground at the same potential.
A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1m². Will he get an electric shock if he touches the metal sheet next morning?
Yes, the man will get an electric shock if he touches the metal slab next morning. The steady discharging current in the atmosphere charges up the aluminium sheet. As a result, its voltage rises gradually. The raise in the voltage depends on the capacitance of the capacitor formed by the aluminium slab and the ground.
The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
The occurrence of thunderstorms and lightning charges the atmosphere continuously. Hence, even with the presence of discharging current of 1800 A, the atmosphere is not discharged completely. The two opposing currents are in equilibrium and the atmosphere remains electrically neutral.
What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint: The earth has an electric field of about 100 Vm⁻¹ at its surface in the downward direction, corresponding to a surface charge density = −10⁻⁹ C m⁻². Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
During lightning and thunderstorm, light energy, heat energy, and sound energy are dissipated in the atmosphere.