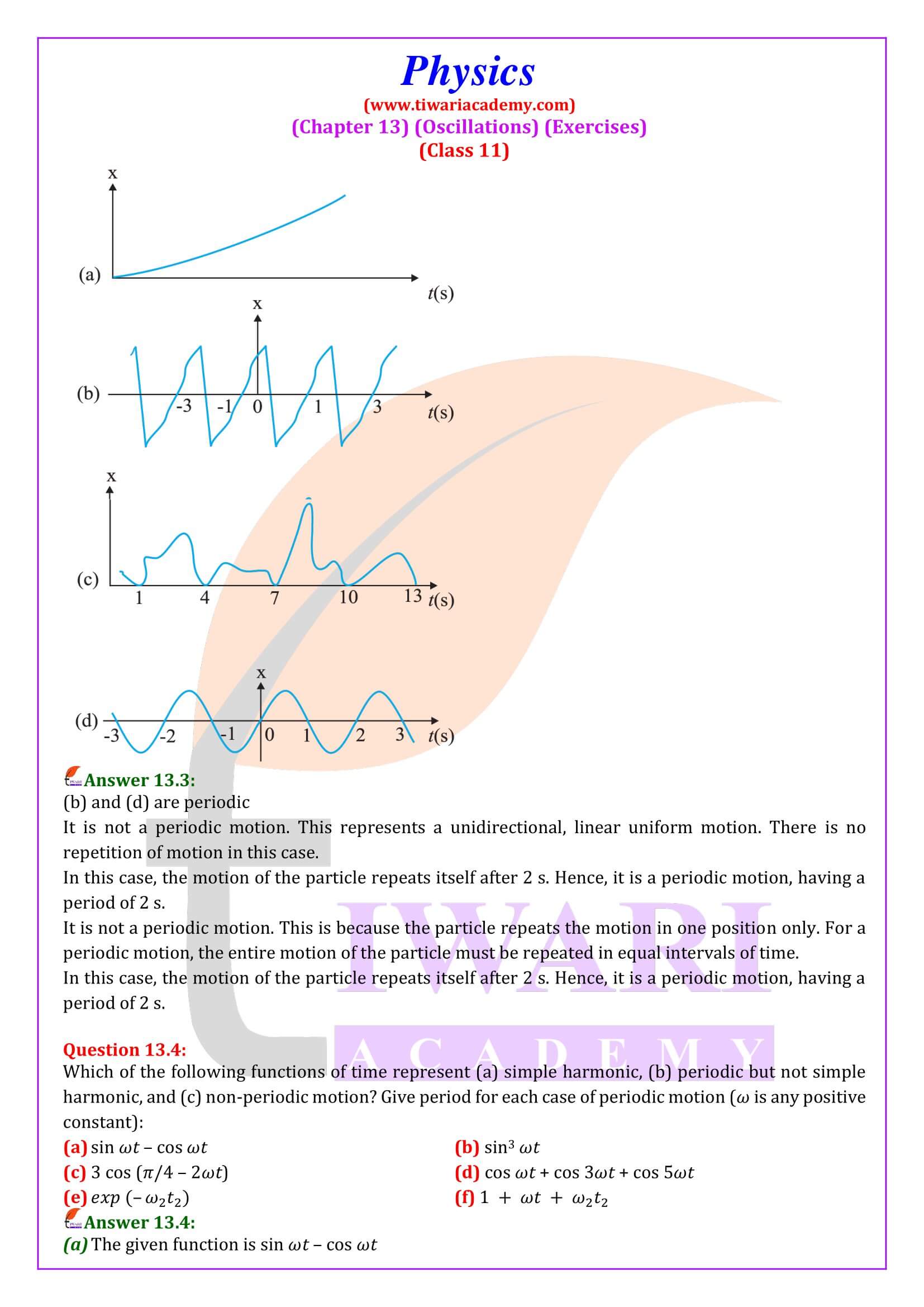
NCERT Solutions for Class 11 Physics Chapter 13 Oscillations in Hindi and English Medium updated for new academic session 2025-26 with MCQ and extra study material. Consistency is key. Regular, focused study sessions are more effective than last-minute cramming. Spread your preparation over a period of time to allow for deeper understanding.
Class 11 Physics Chapter 13 Oscillations Question Answers
Class 11 Physics Chapter 13 MCQ
In dumped oscillation the directions of the restoring force and the resistive force
The displacement y of a particle executing periodic motion is given by y = 4cos²(t/2)sin(1000t). This expression may be considered to be result of superposition of the following number of harmonic motions.
One of the two clocks on the on the earth is controlled by a pendulum and other by a spring. If both the clocks are taken to the moon, then which clock will have the same time – period of the earth?
For a magnet of time period T magnet moment is M, if the magnetic moment becomes one fourth of the initial value, then the time period of the oscillation becomes
Class 11 Physics Chapter 13 Topic – Energy in SHM
The kinetic and potential energies in the SHM vary from zero to maximum. The equation mentioned for SHM says that the speed of the object follows a sinusoidal path, which means that the speed of the object increases and decreases. The speed is zero at the extremes and maximum at the middle Position. The position where the speed is the greatest is the position where the kinetic energy of the object is also the greatest.
For an object of mass m, the speed is v. In a simple harmonic motion, objects reach their limits and gain potential energy. When the object returns to its average position, its speed reaches its maximum value of kinetic energy. So, in this case, potential energy is converted into kinetic energy and vice versa. In ideal simple harmonic motion, energy is conserved. Although it can change form, the total energy remains the same. It is crucial to study these energy and total energy changes to analyze the SHM and its properties.
Class 11 Physics Chapter 13 Multiple Choice Questions
In the case of forced oscillations, which of the following statement is not true?
In damped oscillation, the angular frequency of the oscillator
The acceleration of particle executing S.H.M. when it is at mean position is
In SHM, graph of which of the following is a straight line?
Uniform Circular Motion in 11th Physics Chapter 13
Planar motion occurs when an object moves in two coordinate systems, such as x, y, or y, z, etc. An example of 2D motion is projectile motion, where the object moves in the horizontal and vertical directions. Uniform circular motion is another example of two-dimensional motion, where an object moves in a uniform circular motion and the velocity is constantly changing at each point because the direction of the velocity vector is constantly changing.
Uniform circular motion is the motion of a two-dimensional object moving at a constant speed along a fixed circular direction, but since the direction of the object constantly changes at each point, the speed also changes and the direction of each point is the direction of the tangent. When the object is constantly changing during a circular motion, at each point the object is subjected to a certain acceleration. The acceleration acts on the center of the circle, causing the displacement of the object in the circle. In this situation, the acceleration is called radial acceleration or centripetal acceleration.
Simple Pendulum and its Properties
A device in which a point mass is usually attached to a light, inextensible string and suspended from a constant support is called a pendulum. The average position of a simple pendulum is usually the vertical gain point of the antenna. The length of the pendulum, denoted L, is the vertical distance between the point of suspension and the center of mass of the suspended object, provided that it is the average position. This type of pendulum tends to have a single resonant frequency. Basically, a simple pendulum is a mechanical device that exhibits periodic motion. It has a small circular pendulum suspended at any fixed end by an inextensible thread of length L.
It performs an oscillatory movement, driven by gravity and occurring in a vertical plane. Generally, hanging bobs are at the very end. The strings are mass-less. The time period of the pendulum can be increased by increasing the length of the rope. The time period of the pendulum is independent of the mass of the suspended pendulum. The time period of the pendulum generally depends on the position of the pendulum and the acceleration of gravity, as it is not uniform everywhere place on earth.
Which concept of forced oscillations is explained in 11th Physics chapter 13?
Forced oscillations are those in which an object oscillates under the influence of an external periodic force. Students of class 12 Physics can understand the typical term related to forced oscillations. An important term to remember when learning about forced oscillations is resonance. Resonance occurs when the frequency of the external force is equal to the natural frequency of the oscillator. At this time frequency is known as the resonant frequency. In class 11 Physics chapter 13, all the derivations related to forced oscillations are given with suitable example.
What are the main topics of chapter 13 of class 11 Physics?
The main topics of Chapter 13 in 11th Physics are periodic and oscillatory motion, simple harmonic motion and uniform circular motion. Class 11 Physics chapter 13 also explains about velocity and acceleration in SHM along with the force law of simple harmonic motion. Energy in simple harmonic motion with some systems that perform SHM, damped harmonic motion, forced oscillation and resonance.
Is chapter 13 of class 11 Physics sufficient to learn all about SHM?
In class 11 Physics chapter 13, a brief overview of SHM is given. Simple Harmonic Motion or SHM is periodic motion in which an object repeatedly moves back and forth through an equilibrium or center position. In this way the maximum displacement of one side is equal to the maximum displacement of the other side. In this type of motion, the acceleration and resultant force of the system are proportional to the displacement and act in the opposite direction of the displacement. A pendulum swinging back and forth (from a middle position) is an example of simple harmonic motion.