A straight highway leads to the foot of a tower. A man standing at

Updated on December 6, 2023
by Tiwari Academy

To find the time taken by the car to reach the foot of the tower, we use trigonometry. Let’s denote the height of the tower as h, the initial distance of the car from the tower as d1, and the distance after 6 seconds as d2.
Initial Position (30° Angle of Depression): Using tan(30°) = 1/√3, the equation is 1/√3 = h/d1.
Position After 6 Seconds (60° Angle of Depression): Using tan(60°) = √3, the equation is √3 = h/d2.
Since d1 = h√3 and d2 = h/√3, the distance covered in 6 seconds is h√3 − h/√3. The speed of the car is this distance divided by 6 seconds. To find the time to reach the tower, use the speed and the distance h/√3. The time taken is (h/√3)/speed, which simplifies to 2 seconds. Therefore, it takes the car 2 seconds to reach the foot of the tower from the latter position.

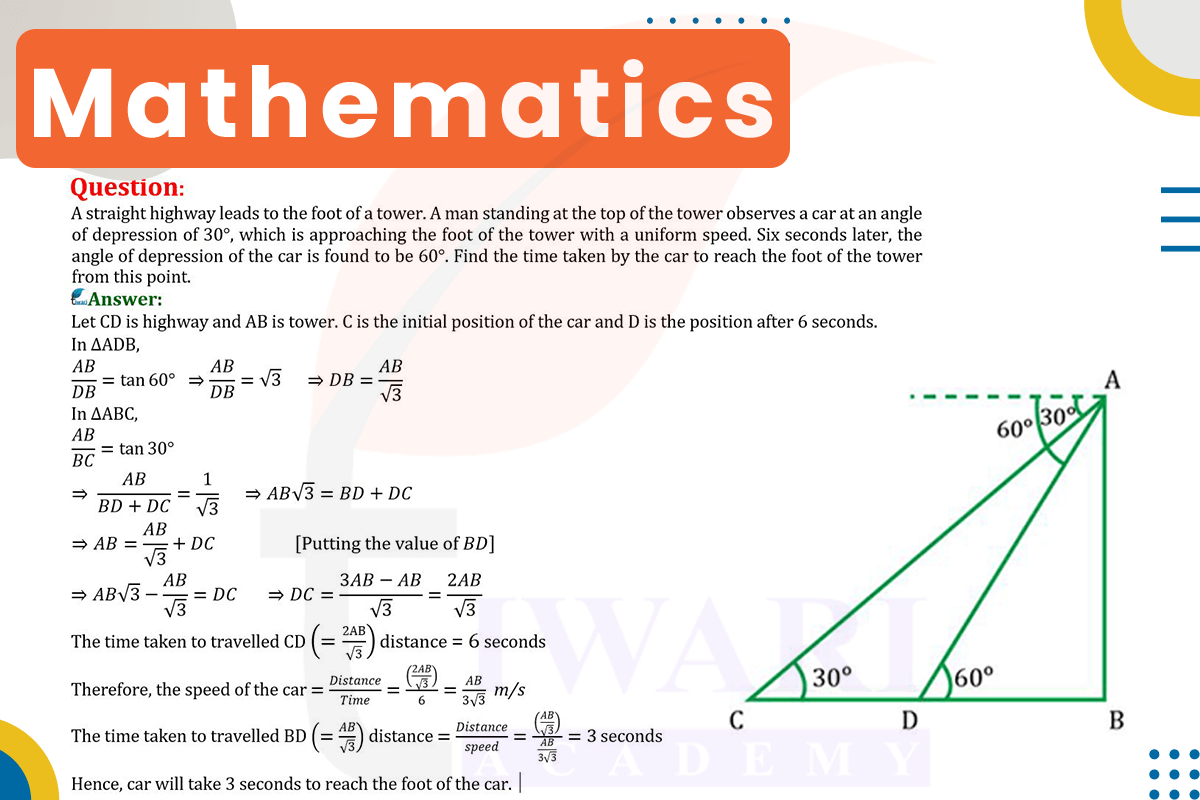
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°.

Let’s discuss in detail

Trigonometric Analysis in Motion Estimation

Trigonometry, a significant branch of mathematics, is often employed in estimating motion and distances, especially in scenarios where direct measurement is not feasible. The problem at hand involves a car approaching a tower, with its angles of depression observed from the tower’s top changing over time. By applying trigonometric principles to these observations, we can estimate the time it will take for the car to reach the tower. This scenario is a practical demonstration of how trigonometry can be applied to solve real-world problems in fields like physics, engineering, and navigation.

Understanding the Problem: Car Approaching a Tower

The problem presents a car moving towards a tower along a straight highway. A man standing at the top of the tower observes the car at an angle of depression of 30°. After six seconds, the angle of depression changes to 60°. The objective is to determine the time it will take for the car to reach the foot of the tower from its position at the 60° angle of depression. This setup forms two right-angled triangles at different instances, one for each angle of depression.

The Role of Tangent in Angle of Depression

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side (height of the tower) to the length of the adjacent side (horizontal distance from the tower). The angles of depression from the tower are equivalent to the angles of elevation from the car to the tower. By applying the tangent function to these angles, we can calculate the car’s distances from the tower at both instances.

Calculating the Initial and Final Distances
For the initial position with a 30° angle of depression, we use the formula tan(30°) = 1/√3. The equation is 1/√3 = h/d1, where d1 is the initial distance. Similarly, for the position after 6 seconds with a 60° angle of depression, the equation is tan(60°) = √3 = h/d2, where d2 is the distance after 6 seconds.

Estimating the Car’s Speed and Time to Reach the Tower

The distance covered by the car in 6 seconds is the difference between d1 and d2, which is h√3 − h/√3. The car’s speed is this distance divided by 6 seconds. To find the time for the car to reach the tower from its position at the 60° angle of depression, we use the speed and the distance h/√3 (the final distance to the tower).

Trigonometry in Determining Time and Distance

The time taken by the car to reach the foot of the tower from the latter position is calculated to be 2 seconds. This example illustrates the practical application of trigonometry in motion estimation and distance calculation, demonstrating its importance in various real-life scenarios. Trigonometry provides a reliable mathematical approach to solving problems where direct measurement of distance and time is challenging, ensuring accuracy and efficiency in planning and analysis.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.