NCERT Exercises Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Updated for New Session 2025-26. Get here all question answers in English and Hindi Medium. As per the NCERT Math textbooks published for 2025-26 Exams, there are only three exercises in chapter 3 of 10th Mathematics.
Select Your Topic Here
► Class 10 Maths Exercise 3.1
► Class 10 Maths Exercise 3.2
► Class 10 Maths Exercise 3.3
The following Study Material includes Class 10 Maths Board Exam Paper questions and practice questions with answer and explanation.
• Board Paper Questions asked from Chapter 3
• Chapter 3 Based Assertion-Reason Type Questions
• Case Study Type Questions with Board Papers
• MCQs based on Linear Equations in Two Variables
Class 10 Maths Chapter 3 One Mark Questions
Class 10 Maths Chapter 3 Two or Three Marks Questions
Class 10 Maths Chapter 3 Three or Four Marks Questions
For Session 2025-26 Class 10 Maths Chapter 3 Solutions
Class 10 Maths Exercise 3.1
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
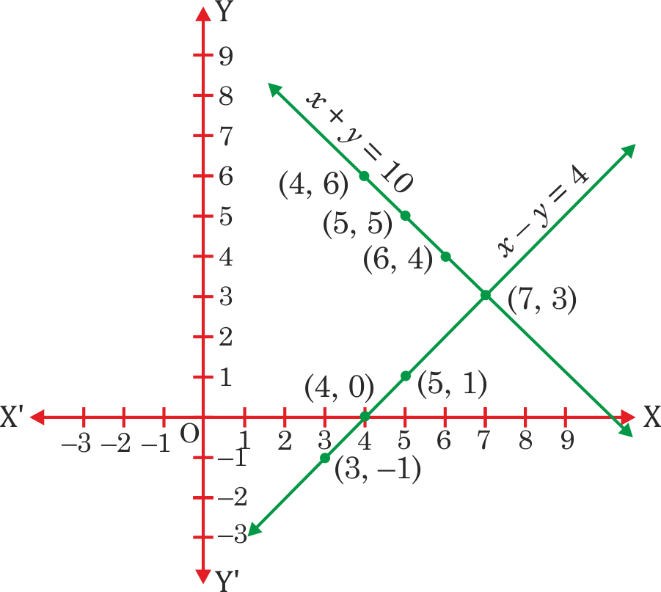
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
See Solution(i) Let the number of girls = x and let the number of boys = y
Total number of students = 10
Therefore,
x + y = 10 …(1)
According to the question, the number of girls is 4 more than the number of boys,
so, x = y + 4 …(2)
To represent graphically, three solutions of each equation is needed.
From equation (1), we get x = 10 – y
x | 5 | 4 | 6
y | 5 | 6 | 4
From equation (2), we get x = y + 4
x | 5 | 4 | 3
y | 1 | 0 | -1
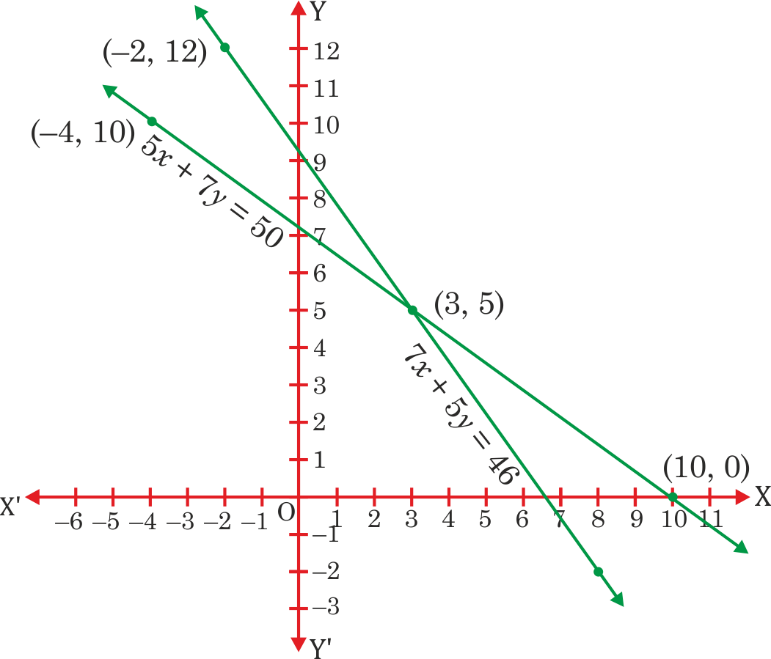
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
See Solution(ii) Let the cost of one pencil = ₹x and the cost of one pen = ₹y
According to the first condition:
5x + 7y = 50 …(1)
According to the second condition:
7x + 5y = 46 …(2)
To represent graphically three solutions of each equation is given below,
From equation (1), we get:
x = (50 – 7y)/5
x | 3 | 10 | -4
y | 5 | 0 | 10
From equation (2), we get:
x = (46 – 5y)/7
x | 7 | 3 | -2
y | 8 | -2 | 12
2. On comparing the ratios a₁/a₂, b₁/b₂ and c₁/c₂, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x − 4y + 8 = 0
7x + 6y − 9 = 0
See Solution(i) 5x − 4y + 8 = 0
7x + 6y − 9 = 0
Here, a₁/a₂ = 5/7 and b₁/b₂ = −4/6 = −2/3
⇒ a₁/a₂ ≠ b₁/b₂
So, the given pairs of linear equations intersect at a point.
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
See Solution(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Here, a₁/a₂ = 9/18 = 1/2,
b₁/b₂ = 3/6 = 1/2, and
c₁/c₂ = 12/24 = 1/2
⇒ a₁/a₂ = b₁/b₂ = c₁/c₂
So, the following pairs of linear equations are coincident.
(iii) 6x − 3y + 10 = 0
2x − y + 9 = 0
See Solution(iii) 6x − 3y + 10 = 0
2x − y + 9 = 0
Here, a₁/a₂ = 6/2 = 3/1,
b₁/b₂ = −3/−1 = 3/1, and
c₁/c₂ = 10/9
⇒ a₁/a₂ = b₁/b₂ ≠ c₁/c₂
So, the following pairs of linear equations are parallel.
3. On comparing the ratios a₁/a₂, b₁/b₂ and c₁/c₂, find out whether the following pairs of linear equations are consistent or inconsistent:
(i) 3x + 2y = 5 ; 2x − 3y = 7
See Solution(i) 3x + 2y = 5
2x − 3y = 7
Here, a₁/a₂ = ³⁄₂ and b₁/b₂ = ²⁄₋₃
⇒ a₁/a₂ ≠ b₁/b₂, so, pair of linear equations are consistent.
(ii) 2x − 3y = 8 ; 4x − 6y = 9
See Solution(ii) 2x − 3y = 8
4x − 6y = 9
Here, a₁/a₂ = ²⁄₄ = ½ , b₁/b₂ = ₋₃⁄₋₆ = ½ , and c₁/c₂ = ⁸⁄₉
⇒ a₁/a₂ = b₁/b₂ ≠ c₁/c₂, so, pair of linear equations are inconsistent.
(iii) (³⁄₂)x + (⁵⁄₃)y = 7 ; 9x − 10y = 14
See Solution(iii) (³⁄₂)x + (⁵⁄₃)y = 7
9x − 10y = 14
Here, a₁/a₂ = (³⁄₂)⁄⁹ = ¹⁄₆ and b₁/b₂ = (⁵⁄₃)⁄₋₁₀ = ₋¹⁄₆
⇒ a₁/a₂ ≠ b₁/b₂, so, pair of linear equations are consistent.
(iv) 5x − 3y = 11 ; −10x + 6y = −22
See Solution(iv) 5x − 3y = 11
−10x + 6y = −22
Here, a₁/a₂ = ⁵⁄₋₁₀ = ₋½ , b₁/b₂ = ₋³⁄₆ = ₋½ , and c₁/c₂ = ¹¹⁄₋₂₂ = ₋½
⇒ a₁/a₂ = b₁/b₂ = c₁/c₂, so, pair of linear equations are consistent.
(v) (⁴⁄₃)x + 2y = 8 ; 2x + 3y = 12
See Solution(v) (⁴⁄₃)x + 2y = 8
2x + 3y = 12
Here, a₁/a₂ = (⁴⁄₃)⁄₂ = ²⁄₃ , b₁/b₂ = ²⁄₃ and c₁/c₂ = ⁸⁄₁₂ = ²⁄₃
⇒ a₁/a₂ = b₁/b₂ = c₁/c₂, so, pair of linear equations are consistent.
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
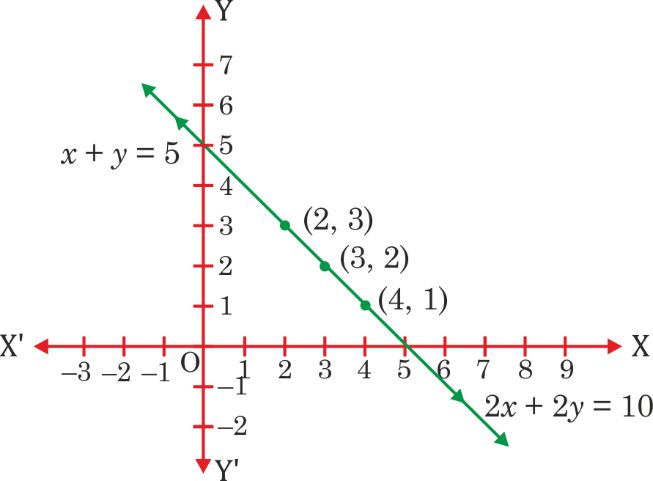
(i) x + y = 5, 2x + 2y = 10
See Solution(i) x + y = 5 …(1)
2x + 2y = 10 …(2)
Here, a₁/a₂ = 1/2, b₁/b₂ = 1/2, and c₁/c₂ = 5/10 = 1/2
⇒ a₁/a₂ = b₁/b₂ = c₁/c₂, so, pairs of linear equations are consistent.
For three solutions of each equation,
From equation (1), we get, x = 5 − y
x | 4 | 3 | 2
y | 1 | 2 | 3
From equation (2), we get, x = (10 − 2y)/2
x | 4 | 3 | 2
y | 1 | 2 | 3
(ii) x − y = 8, 3x − 3y = 16
See Solution(ii) x − y = 8 …(1)
3x − 3y = 16 …(2)
Here, a₁/a₂ = 1/3,
b₁/b₂ = -1/-3 = 1/3, and c₁/c₂ = 8/16 = 1/2
⇒ a₁/a₂ = b₁/b₂ ≠ c₁/c₂, so, pairs of linear equations are inconsistent.
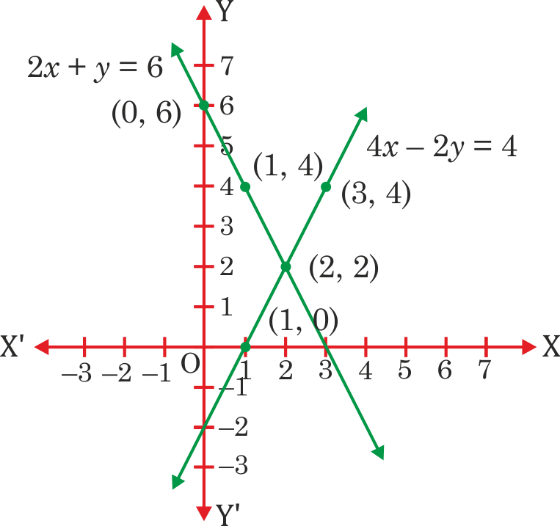
(iii) 2x + y − 6 = 0, 4x − 2y − 4 = 0
See Solution(iii) 2x + y − 6 = 0 …(1)
4x − 2y − 4 = 0 …(2)
Here, a₁/a₂ = 2/4 = 1/2 and b₁/b₂ = 1/(-2) = -1/2
⇒ a₁/a₂ ≠ b₁/b₂, so, pairs of linear equations are consistent/inconsistent
For three solutions of each equation,
From equation (1), we get, x = (6 − y)/2
x | 0 | 1 | 2
y | 6 | 4 | 2
From equation (2), we get, x = (4 + 2y)/4
x | 1 | 2 | 3
y | 0 | 2 | 4
(iv) 2x − 2y − 2 = 0, 4x − 4y − 5 = 0
See Solution(iv) 2x − 2y − 2 = 0 …(1)
4x − 4y − 5 = 0 …(2)
Here, a₁/a₂ = 2/4 = ¹⁄₂,
b₁/b₂ = (−2)/(−4) = ¹⁄₂, and c₁/c₂ = (−2)/(−5) = ²⁄₅
⇒ a₁/a₂ = b₁/b₂ ≠ c₁/c₂, so, pairs of linear equations are inconsistent.
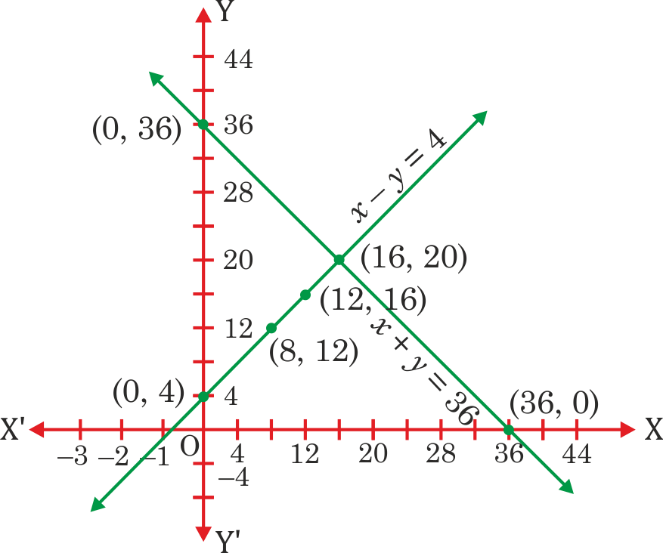
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
See AnswerLet the breadth of garden = x m and let the length of the garden = y m
Half of the perimeter = 36 m
⇒ 1/2 [2(x + y)] = 36
⇒ x + y = 36 … (1)
According to question, length is 4 m more than its width, so
y = x + 4 … (2)
To get three solutions of each equation,
Form the equation (1), we get x = 36 – y
x | 0 | 36 | 16
y | 36 | 0 | 20
From the equation (2), we get y = x + 4
x | 0 | 8 | 12
y | 4 | 8 | 16
6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
See Solution(i) Given line 2x + 3y – 8 = 0 intersect the line x + 3y – 10 = 0, as
a₁/a₂ ≠ b₁/b₂
(ii) Given line 2x + 3y – 8 = 0 is parallel to 4x + 6y – 9 = 0, as
a₁/a₂ = b₁/b₂ ≠ c₁/c₂
(iii) Given line 2x + 3y – 8 = 0 is coincident to 4x + 6y – 16 = 0, as
a₁/a₂ = b₁/b₂ = c₁/c₂
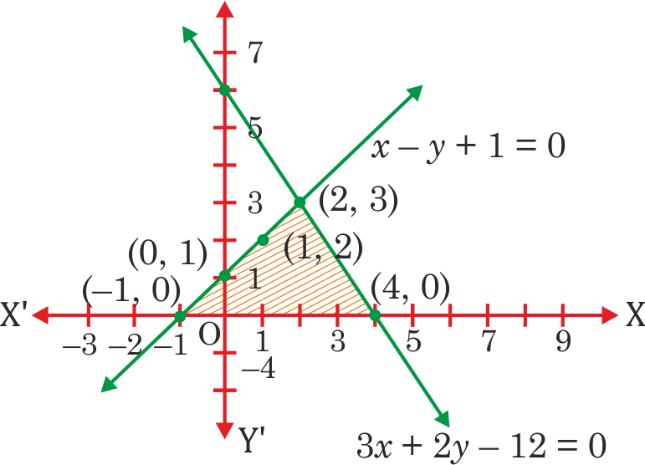
7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
See SolutionFrom the equation (1), we get x = y – 1
x | 0 | 1 | 2
y | 1 | 2 | 3
From the equation (2), we get x = (12 – 2y)/3
x | 4 | 2 | 0
y | 0 | 3 | 6
The coordinates of the vertices of the triangle formed by these lines and the x-axis are (-1, 0), (4, 0) and (2, 3).
Class 10 Maths Exercise 3.2
1. Solve the following pair of linear equations by the substitution method:
(i) x + y = 14; x – y = 4
See Solution(i) x + y = 14 … (1)
x – y = 4 … (2)
From the equation (1), we get
y = 14 – x … (3)
Putting the value of y in equation (2), we get
x – (14 – x) = 4
⇒ 2x = 18
⇒ x = 9
Putting the value of x in equation (3), we get
y = 14 – 9 = 5
Hence, x = 9 and y = 5.
(ii) s – t = 3; s/3 + t/2 = 6
See Solution(ii) s – t = 3 … (1)
s/3 + t/2 = 6 … (2)
From the equation (1), we get
s = 3 + t … (3)
Putting the value of s in equation (2), we get
(3 + t)/3 + t/2 = 6
⇒ (6 + 2t + 3t) / 6 = 6
⇒ 5t + 6 = 36
⇒ t = 6
Putting the value of t in equation (3), we get
s = 3 + 6 = 9
Hence, s = 9 and t = 6.
(iii) 3x – y = 3; 9x – 3y = 9
See Solution(iii) 3x – y = 3 … (1)
9x – 3y = 9 … (2)
From the equation (1), we get
y = 3x – 3 … (3)
Putting the value of y in equation (2), we get
9x – 3(3x – 3) = 9
⇒ 9 = 9, which is true.
Hence, pair of linear equations have infinite many solution.
(iv) 0.2x + 0.3y = 1.3; 0.4x + 0.5y = 2.3
See Solution(iv) 0.2x + 0.3y = 1.3 … (1)
0.4x + 0.5y = 2.3 … (2)
From the equation (1), we get
y = (1.3 – 0.2x) / 0.3 … (3)
Putting the value of y in equation (2), we get
0.4x + 0.5 [( (1.3 – 0.2x) / 0.3 )] = 2.3
⇒ 0.12x + 0.65 – 0.10x = 0.69
⇒ 0.02x = 0.04
⇒ x = 2
Putting the value of x in equation (3), we get
y = (1.3 – 0.2(2)) / 0.3 = 0.9 / 0.3 = 3
Hence, x = 2 and y = 3.
(v) √2x + √3y = 0; √3x – √2y = 0
See Solution(v) √2x + √3y = 0 … (1)
√3x – √2y = 0 … (2)
From the equation (1), we get
y = -√2x / √3 … (3)
Putting the value of y in equation (2), we get
√3x – √2 [(-√2x / √3)] = 0
⇒ 3x + 2x = 0
⇒ x = 0
Putting the value of x in equation (3), we get
y = 0
Hence, x = 0 and y = 0.
(vi) 3x/2 – 5y/3 = -2; x/3 + y/2 = 13/6
See Solution(vi) 3x/2 – 5y/3 = -2 … (1)
x/3 + y/2 = 13/6 . .. (2)
From the equation (1), we get,
5y/3 = 3x/2 + 2 = (3x + 4)/2
y = (3/5) [((3x+4)/2)] = (9x+12)/10 … (3)
Putting the value of y in equation (2), we get
x/3 + (1/2) [((9x + 12)/10)] = 13/6
⇒ (20x + 27x + 36) / 60 = 13/6
⇒ 282x + 216 = 780
⇒ 282x = 564
⇒ x = 2
Putting the value of x in equation (3), we get
y = (9(2) + 12) / 10
= (18 + 12) / 10
= 30 / 10 = 3
Hence, x = 2 and y = 3.
2. Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which y = mx + 3.
See Solution2x + 3y = 11 … (1)
2x – 4y = -24 … (2)
From the equation (1), we get
y = (11 – 2x) / 3 … (3)
Putting the value of y in equation (2), we get
2x – 4 [( (11 – 2x) / 3)] = -24
⇒ 6x – 44 + 8x = -72
⇒ 14x = -28
⇒ x = -2
Putting the value of x in equation (3), we get
y = (11 – 2(-2))/3 = (11 + 4)/3 = 15/3 = 5
Hence, x = -2 and y = 5.
Putting the value of x and y in y = mx + 3, we get
5 = m(-2) + 3
⇒ 5 = -2m + 3
⇒ 2m = -2
⇒ m = -1
3. Form the pair of linear equations for the following problems and find their solution by substitution method:
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
See Solution(i) Let the first number = x
Let the second number = y
According to question,
x = 3y … (1)
The difference between two number is 26, therefore
x – y = 26 … (2)
Putting the value of x in equation (2), we get
3y – y = 26
=> 2y = 26
=> y = 13
Putting the value of y in equation (1), we get
x = 3(13) = 39
Hence, one number is 13 and the other number is 39.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
See Solution(ii) Let the larger angle = x
Let the smaller angle = y
According to question,
x = y + 18 … (1)
Both angles are supplementary, therefore
x + y = 180 … (2)
Putting the value of x in equation (2), we get
y + 18 + y = 180
=> 2y + 18 = 180
=> 2y = 162
=> y = 81
Putting the value of y in equation (1), we get
x = 81 + 18 = 99
Hence, one angle is 81° and the other one is 99°.
(iii) The coach of a cricket team buys 7 bats and 6 balls for ₹3800. Later, she buys 3 bats and 5 balls for ₹1750. Find the cost of each bat and each ball.
See Solution(iii) Let the cost of one bat = ₹x
Let the cost of one ball = ₹y
According to first condition,
7x + 6y = 3800
=> x = (3800 – 6y) / 7 … (1)
According to second condition,
3x + 5y = 1750 … (2)
Putting the value of x in equation (2), we get
3 [(3800 – 6y) / 7] + 5y = 1750
(11400 – 18y) / 7 + 5y = 1750
11400 – 18y + 35y = 12250
11400 + 17y = 12250
=> 17y = 850
=> y = 50
Putting the value of y in equation (1), we get
x = [3800 – 6 (50)] / 7
x = (3800 – 300) / 7
x = 3500 / 7
x = 500
Hence, the cost of one bat is ₹500 and the cost of one ball is ₹50.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ₹105 and for a journey of 15 km, the charge paid is ₹155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
See Solution(iv) Let the fixed charges = ₹x
Let the charge per kilometre = ₹y
According to first condition, for travelling 10 km,
x + 10y = 105
=> x = 105 – 10y … (1)
According to second condition, for travelling 15 km,
x + 15y = 155 … (2)
Putting the value of x in equation (2), we get
(105 – 10y) + 15y = 155
=> 105 + 5y = 155
=> 5y = 50
=> y = 10
Putting the value of y in equation (1), we get
x = 105 – 10 (10) = 105 – 100 = 5
So, the fixed charges x = ₹5 and charge per km y = ₹10.
Therefore, the charges for 25 km = x + 25y = ₹[5 + 25(10)] = ₹(5 + 250) = ₹255
(v) A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6. Find the fraction.
See Solution(v) Let the numerator = x
Let the denominator = y
Therefore, the fraction = x/y
According to first condition,
(x + 2) / (y + 2) = 9/11 => 11(x + 2) = 9(y + 2) => 11x + 22 = 9y + 18
=> 11x – 9y = -4
=> x = (9y – 4) / 11 … (1)
According to second condition,
(x + 3) / (y + 3) = 5/6
=> 6(x + 3) = 5(y + 3)
=> 6x + 18 = 5y + 15
=> 6x – 5y = -3 … (2)
Putting the value of x in equation (2), we get
6 [(9y – 4) / 11] – 5y = -3
(54y – 24) / 11 – 5y = -3
54y – 24 – 55y = -33
=> -y – 24 = -33
=> -y = -9 => y = 9
Putting the value of y in equation (1), we get
x = [9(9) – 4] / 11 = (81 – 4) / 11 = 77 / 11 = 7
Hence, the fraction = x/y = 7/9.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
See Solution(vi) Let the age of Jacob = x years
Let the age of son = y years
After 5 years,
Jacob’s age = x + 5 years
Son’s age = y + 5 years
According to question,
x + 5 = 3(y + 5)
=> x + 5 = 3y + 15
=> x = 3y + 10 … (1)
5 years ago,
Jacob’s age = x – 5 years
Son’s age = y – 5 years
According to question,
x – 5 = 7(y – 5)
=> x – 5 = 7y – 35
=> x – 7y = -30 … (2)
Putting the value of x in equation (2), we get
3y + 10 – 7y = -30
=> -4y + 10 = -30
=> -4y = -40
=> y = 10
Putting the value of y in equation (1), we get
x = 3(10) + 10 = 30 + 10 = 40
Hence, the age of Jacob is 40 years and the age of his son is 10 years.
Class 10 Maths Exercise 3.3
1. Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
See Solution(i) x + y = 5 … (1)
2x – 3y = 4 … (2)
Multiply equation (1) by 2 and subtracting from equation (2), we get
– 5y = -6
=> y = 6/5
Putting the value of y in equation (1), we get
x + 6/5 = 5
=> x = 5 – 6/5 = (25 – 6)/5
=> x = 19/5
Hence, x = 19/5 and y = 6/5.
(ii) 3x + 4y = 10 and 2x – 2y = 2
See Solution(ii) 3x + 4y = 10 … (1)
2x – 2y = 2 … (2)
Multiply equation (2) by 2 and adding with equation (1), we get
7x = 14
=> x = 14/7 = 2
Putting the value of x in equation (1), we get
3(2) + 4y = 10
=> 6 + 4y = 10
=> 4y = 4
=> y = 1
Hence, x = 2 and y = 1.
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
See Solution(iii) 3x – 5y – 4 = 0 … (1)
9x – 2y = 7 … (2)
Multiply equation (1) by 3 and subtracting from equation (2), we get
13y = -5
=> y = -5/13
Putting the value of y in equation (2), we get
9x – 2(-5/13) = 7
=> 9x + 10/13 = 7
=> 9x = 7 – 10/13 = (91 – 10)/13 = 81/13
=> x = (81/13) / 9 = 81/[13(9) = 9/13
Hence, x = 9/13 and y = -5/13.
(iv) x/2 + 2y/3 = -1 and x – y/3 = 3
See Solution(iv) x/2 + 2y/3 = -1
=> 3x + 4y = -6 … (1)
and x – y/3 = 3
=> 3x – y = 9 … (2)
Subtracting equation (1) from equation (2), we get
5y = -15
=> y = -3
Putting the value of y in equation (1), we get
3x + 4(-3) = -6
=> 3x – 12 = -6
=> 3x = 6
=> x = 2
Hence, x = 2 and y = -3.
2. Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to the denominator. What is the fraction?
See Solution(i) Let the numerator = x
Let the denominator = y
Therefore, the fraction = x/y
According to first condition,
(x + 1) / (y – 1) = 1
=> x + 1 = y – 1
=> x – y = -2 … (1)
According to second condition,
x / (y + 1) = 1/2
=> 2x = y + 1
=> 2x – y = 1 … (2)
Multiply equation (1) by 2 and subtracting from equation (2), we get
y = 5
Putting the value of y in equation (1), we get
x – 5 = -2
=> x = -2 + 5
=> x = 3
Hence, the fraction = x/y = 3/5.
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
See Solution(ii) Let the age of Nuri = x years
Let the age of Sonu = y years
5 years ago,
Age of Nuri = x – 5 years
Age of Sonu = y – 5 years
According to question, x – 5 = 3(y – 5)
=> x – 5 = 3y – 15
=> x – 3y = -10 … (1)
After 10 years,
Age of Nuri = x + 10 years
Age of Sonu = y + 10 years
According to question, x + 10 = 2(y + 10)
=> x + 10 = 2y + 20
=> x – 2y = 10 … (2)
Subtracting equation (2) from equation (1), we get
-y = -20
=> y = 20
Putting the value of y in equation (1), we get
x – 3(20) = -10
=> x – 60 = -10
=> x = 50
Hence, age of Nuri is 50 years age of Sonu is 20 years.
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
See Solution(iii) Let the one’s place = x
Let the ten’s place = y
Therefore, the number = 10y + x
Sum of digits is 9, therefore
x + y = 9 … (1)
Number obtained by reversing the digits = 10x + y
According to question,
9(10y + x) = 2(10x + y)
=> 90y + 9x = 20x + 2y
=> 88y – 11x = 0
=> 11x – 88y = 0
=> x – 8y = 0 … (2)
Subtracting equation (2) from equation (1), we get
9y = 9
=> y = 1
Putting the value of y in equation (1), we get
x + 1 = 9
=> x = 8
Therefore, the number = 10y + x = 10(1) + 8 = 18
Hence, the two digit number is 18.
(iv) Meena went to a bank to withdraw ₹2000. She asked the cashier to give her ₹50 and ₹100 notes only. Meena got 25 notes in all. Find how many notes of ₹50 and ₹100 she received.
See Solution(iv) Let the number of notes of ₹50 = x
Let the number of notes of ₹100 = y
Total number of notes is 25, therefore
x + y = 25 … (1)
The total amount of ₹50 and ₹100 is ₹2000, therefore
50x + 100y = 2000
=> x + 2y = 40 … (2)
Subtracting equation (1) from equation (2), we get
y = 15
Putting the value of y in equation (1), we get
x + 15 = 25
=> x = 10
Hence, the number of ₹50 notes is 10 and the number of ₹100 is 15.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹27 for a book kept for seven days, while Susy paid ₹21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
See Solution(v) Let the charge for first three days = ₹x
Let the additional charge for each day = ₹y
Charge for seven days is ₹27, therefore
x + 4y = 27 … (1)
Charge for 5 days is ₹21, therefore
x + 2y = 21 … (2)
Subtracting equation (2) from equation (1), we get
2y = 6
=> y = 3
Putting the value of y in equation (1), we get
x + 4(3) = 27
=> x + 12 = 27
=> x = 15
Hence, the fixed charge is ₹15 and the additional charge for each day is ₹3.
Class 10 Maths Chapter 3 Board Questions
Previous Years Questions from CBSE Board Exams based on Class 10 Maths Chapter 3 Pair of Liner Equations in Two Variables are given here with answer and explanation. Past Years Exams questions are important to prepare for school test and to cross-check your knowledge about the chapter.
Class 10 Maths Chapter 3 Previous Year’s Questions
1. Solve the following system of equations algebraically: 30x + 44y = 19; 40x + 55y = 13. [CBSE 2025]
See AnswerMultiplying the first equation by 2: 60x + 88y = 38
Multiplying the second equation by 3: 120x + 165y = 39
Subtracting the first from the second: 60x + 77y = 1
From 60x + 88y = 38:
60x = 38 – 88y
x = (38 – 88y)/60
Substituting into 60x + 77y = 1:
60((38 – 88y)/60) + 77y = 1
38 – 88y + 77y = 1
38 – 11y = 1
-11y = 1 – 38 = -37
y = 37/11
Substituting back: x = (38 – 88(37/11))/60
x = (38 – 296)/60
x = -258/60 = -43/10
Therefore, x = -43/10 and y = 37/11
2. The monthly incomes of two persons are in the ratio 9:7 and their monthly expenditures are in the ratio 4:3. If each saved ₹5,000, express the given situation algebraically as a system of linear equations in two variables. Hence, find their respective monthly incomes. [CBSE 2025]
See AnswerLet’s denote:
x = monthly income of the first person
y = monthly income of the second person
x – 5000 = expenditure of first person
y – 5000 = expenditure of second person
Given:
x/y = 9/7 (income ratio)
(x – 5000)/(y – 5000) = 4/3 (expenditure ratio)
From the first equation: x = (9/7)y
From the second equation: (x – 5000)/(y – 5000) = 4/3
3(x – 5000) = 4(y – 5000)
3x – 15000 = 4y – 20000
3x – 4y = -5000
Substituting x = (9/7)y into the equation:
3(9/7)y – 4y = -5000
27y/7 – 4y = -5000
27y/7 – 28y/7 = -5000
-y/7 = -5000
y = 35000
Now find x:
x = (9/7)y = (9/7) × 35000 = 45000
Therefore, the monthly incomes are ₹45,000 and ₹35,000.
3. If 2x + y = 13 and 4x – y = 17, then find the value of (x – y). [CBSE 2024]
See SolutionAdding the two equations: 2x + y = 13 and 4x – y = 17
6x = 30
Therefore, x = 5
Substituting x = 5 into the first equation: 2(5) + y = 13
10 + y = 13
y = 3
Now I can find (x – y): x – y = 5 – 3 = 2
Therefore, (x – y) = 2
4. Solve the following system of linear equations graphically: x – y + 1 = 0 and x + y = 5 [CBSE 2024]
See SolutionRearranging the equations:
x – y = -1 …(1)
x + y = 5 …(2)
For equation (1): x-intercept (when y = 0): x = -1 y-intercept (when x = 0): -y = -1, so y = 1
For equation (2): x-intercept (when y = 0): x = 5 y-intercept (when x = 0): y = 5
When plotted, these lines intersect at (2, 3), which can be verified by substituting into both equations.
Therefore, the solution is x = 2, y = 3.
5. Sum of two numbers is 105 and their difference is 45. Find the numbers. [CBSE 2024]
See SolutionLet the two numbers be a and b.
Given:
a + b = 105 …(1)
and
a – b = 45 …(2)
Adding equations (1) and (2):
2a = 150
a = 75
Substituting a = 75 in equation (1):
75 + b = 105
b = 30
Therefore, the two numbers are 75 and 30.
6. Two peoples are 16 km apart on a straight road. They start walking at the same time. If they walk towards each other with different speeds, they will meet in 2 h. Had they walked in the same direction with same speeds as before, they would have met in 8 h. Find their walking speeds. [CBSE 2024]
See SolutionLet their speeds be u km/h and v km/h.
When they walk towards each other:
(u + v) × 2 = 16
u + v = 8 …(1)
When they walk in the same direction:
|u – v| × 8 = 16
|u – v| = 2
Since we don’t know which speed is greater, let’s assume u > v:
u – v = 2 …(2)
Solving equations (1) and (2):
u + v = 8
u – v = 2
2u = 10
u = 5
Substituting back:
5 + v = 8
v = 3
Therefore, their walking speeds are 5 km/h and 3 km/h.
7. A fraction becomes 1/3 when 1 is subtracted from the numerator. It becomes 1/4 when 8 is added to the denominator. Find the fraction. [CBSE 2023]
See SolutionLet the fraction be x/y.
From the first condition:
(x – 1)/y = 1/3
3(x – 1) = y
3x – 3 = y …(1)
From the second condition:
x/(y + 8) = 1/4
4x = y + 8 …(2)
Substituting equation (1) into equation (2):
4x = 3x – 3 + 8
4x = 3x + 5
x = 5
Using equation (1): y = 3x – 3 = 3(5) – 3 = 15 – 3 = 12
Therefore, the fraction is 5/12.
8. The age of the father is twice the sum of the ages of his two children. After 20 yr, his age will be equal to the sum of the ages of his children. Find the present age of the father. [CBSE 2023 Compt]
See SolutionLet the present ages of the two children be a and b years, and the father’s present age be F years.
Given:
F = 2(a + b) …(1)
F + 20 = (a + 20) + (b + 20) …(2)
Simplifying equation (2):
F + 20 = a + b + 40
F = a + b + 20 …(3)
From equations (1) and (3): 2(a + b) = a + b + 20
a + b = 20
Substituting back into equation (1): F = 2(20) = 40
Therefore, the present age of the father is 40 years.
9. Solve the following pair of equations graphically: x + 3y = 6, 2x – 3y = 12. Also, find the area of the triangle formed by these lines representing the equations with Y-axis. [CBSE 2023 Compt]
See SolutionFor x + 3y = 6: x-intercept (y = 0): x = 6 y-intercept (x = 0): y = 2
For 2x – 3y = 12: x-intercept (y = 0): x = 6 y-intercept (x = 0): y = -4
The lines intersect at (6, 0), which can be verified by substitution.
The triangle formed with the Y-axis has vertices at (0, 2), (0, -4) and (6, 0).
The area of this triangle
= (1/2) × base × height
= (1/2) × 6 × (2 – (-4))
= (1/2) × 6 × 6
= 18 square units.
10. In a ΔABC, ∠A = x°, ∠B = (3x – 2)° and ∠C = y°. Also, ∠C – ∠B = 9°. Determine the three angles of the triangle. [CBSE 2023 Compt]
See SolutionGiven: ∠A = x° ∠B = (3x – 2)° ∠C = y° ∠C – ∠B = 9°
Since the angles in a triangle sum to 180°: x + (3x – 2) + y = 180 …(1)
From ∠C – ∠B = 9°:
y – (3x – 2) = 9
y = 3x – 2 + 9
y = 3x + 7 …(2)
Substituting equation (2) into equation (1):
x + (3x – 2) + (3x + 7) = 180
x + 3x – 2 + 3x + 7 = 180
7x + 5 = 180
7x = 175
x = 25
Now we can find the other angles:
∠B = 3x – 2 = 3(25) – 2 = 75 – 2 = 73°
∠C = y = 3x + 7 = 3(25) + 7 = 75 + 7 = 82°
To verify: ∠A + ∠B + ∠C = 25° + 73° + 82° = 180°
Also, ∠C – ∠B = 82° – 73° = 9°
Therefore, the three angles of the triangle are 25°, 73° and 82°.
11. Solve the equations x + 2y = 6 and 2x – 5y = 12 graphically. [CBSE 2020]
See SolutionTo solve graphically, we’ll find the intercepts for each equation and plot them.
For equation x + 2y = 6: x-intercept (when y = 0): x = 6 y-intercept (when x = 0): 2y = 6, so y = 3
For equation 2x – 5y = 12: x-intercept (when y = 0): 2x = 12, so x = 6 y-intercept (when x = 0): -5y = 12, so y = -2.4
Plotting these points and drawing the lines, they intersect at (6, 0).
Therefore, the solution is x = 6, y = 0, which can be verified by substituting into both equations.
12. If 2x + y = 23 and 4x – y = 19, then find the value of (5y – 2x) and (y/x – 2). [CBSE 2020]
See SolutionSolving the system of equations:
2x + y = 23 …(1) and
4x – y = 19 …(2)
Adding equations (1) and (2):
6x = 42
x = 7
Substituting x = 7 into equation (1):
2(7) + y = 23
14 + y = 23
y = 9
Now I can calculate: (5y – 2x) = 5(9) – 2(7) = 45 – 14 = 31
(y/x – 2) = (9/7) – 2 = (9/7) – (14/7) = -5/7
Therefore, (5y – 2x) = 31 and (y/x – 2) = -5/7.
13. A man can row a boat downstream 20 km in 2 h and upstream 4 km in 2 h. Find his speed of rowing in still water. Also, find the speed of the stream. [CBSE 2020]
See SolutionLet the man’s rowing speed in still water be u km/h and the stream’s speed be v km/h.
For downstream:
(u + v) × 2 = 20
u + v = 10 …(1)
For upstream:
(u – v) × 2 = 4
u – v = 2 …(2)
Solving equations (1) and (2):
u + v = 10
u – v = 2
Adding (1) and (2)
2u = 12
u = 6
Substituting back:
6 + v = 10
v = 4
Therefore, the man’s rowing speed in still water is 6 km/h, and the stream’s speed is 4 km/h.
14. It can take 12 h to fill a swimming pool using two pipes. If the pipe of largest diameter is used for four hour and the pipe of smaller diameter for 9 h, only half of the pool can be filled. How long would it take for each pipe to fill the pool separately? [CBSE 2020]
See SolutionLet’s say the larger pipe can fill the pool in x hours and the smaller pipe can fill it in y hours.
In 1 hour, the larger pipe fills 1/x of the pool and the smaller pipe fills 1/y of the pool.
From the first condition (both pipes fill the pool in 12 hours):
(1/x + 1/y) × 12 = 1 1/x + 1/y = 1/12 …(1)
From the second condition (large pipe for 4 hours and small pipe for 9 hours fill half the pool): (1/x × 4) + (1/y × 9) = 1/2 4/x + 9/y = 1/2 …(2)
Multiplying equation (1) by 12: 12/x + 12/y = 1 …(3)
From equation (2) × 2: 8/x + 18/y = 1 …(4)
Subtracting equation (4) from equation (3):
4/x – 6/y = 0
4/x = 6/y
2/x = 3/y
2y = 3x
y = 3x/2 …(5)
Substituting equation (5) into equation (1):
1/x + 1/(3x/2) = 1/12
1/x + 2/(3x) = 1/12
(3 + 2)/3x = 1/12
5/(3x) = 1/12
5 = 3x/12
x = 20
Using equation (5):
y = 3x/2 = 3(20)/2 = 30
Therefore, it would take the larger pipe 20 hours and the smaller pipe 30 hours to fill the pool separately.
15. Determine graphically the coordinates of the vertices of a triangle, the equations of whose sides are given by 2y – x = 8, 5y – x = 14 and y – 2x = 1. [CBSE 2020]
See SolutionTo find the vertices of the triangle, I need to find the points of intersection of the three lines:
Line 1: 2y – x = 8 → x = 2y – 8
Line 2: 5y – x = 14 → x = 5y – 14
Line 3: y – 2x = 1 → y = 2x + 1
For the first vertex (intersection of lines 1 and 2): 2y – 8 = 5y – 14 -3y = -6 y = 2 Substituting y = 2 into line 1: x = 2(2) – 8 = 4 – 8 = -4 Vertex 1: (-4, 2)
For the second vertex (intersection of lines 2 and 3): 5y – 14 = x 2x + 1 = y Substituting: 5(2x + 1) – 14 = x 10x + 5 – 14 = x 10x – x = 14 – 5 9x = 9 x = 1 y = 2(1) + 1 = 3 Vertex 2: (1, 3)
For the third vertex (intersection of lines 1 and 3): 2y – 8 = x y = 2x + 1 Substituting: 2(2x + 1) – 8 = x 4x + 2 – 8 = x 4x – x = 8 – 2 3x = 6 x = 2 y = 2(2) + 1 = 5 Vertex 3: (2, 5)
Therefore, the coordinates of the triangle’s vertices are (-4, 2), (1, 3) and (2, 5).
16. A father’s age is three times the sum of the ages of his two children. After 5 yr his age will be two times the sum of their ages. Find the present age of the father. [CBSE 2019]
See SolutionLet the present ages of the two children be x and y years. Then the father’s present age = 3(x + y) years.
After 5 years:
The children’s ages will be (x + 5) and (y + 5) years
The father’s age will be 3(x + y) + 5 years
According to the second condition:
3(x + y) + 5 = 2[(x + 5) + (y + 5)]
3(x + y) + 5 = 2(x + y + 10)
3(x + y) + 5 = 2(x + y) + 20
3(x + y) – 2(x + y) = 20 – 5
(x + y) = 15
This means the sum of the children’s ages is 15 years. Therefore, the father’s present age = 3(15) = 45 years.
17. A fraction becomes 1/3 when 2 is subtracted from the numerator and it becomes 1/5 when 1 is subtracted from the denominator. Find the fraction. [CBSE 2019]
See SolutionLet the fraction be x/y where x is the numerator and y is the denominator.
According to the first condition:
(x – 2)/y = 1/3
x – 2 = y/3
3x – 6 = y
According to the second condition:
x/(y – 1) = 1/5
5x = y – 1
From the second equation: y = 5x + 1
Substituting this into the first equation:
3x – 6 = 5x + 1
-2x = 7
x = -7/2
Since a fraction should have positive values for a meaningful answer, this solution isn’t appropriate. Let’s double-check our approach.
Actually, we can solve this differently. From the first condition:
(x – 2)/y = 1/3
3(x – 2) = y
3x – 6 = y
From the second condition:
x/(y – 1) = 1/5
5x = y – 1
y = 5x + 1
Now we have two equations for y:
3x – 6 = 5x + 1
-2x = 7
x = -7/2
Since x = -7/2, then y = 3(-7/2) – 6 = -21/2 – 6 = -21/2 – 12/2 = -33/2
The fraction x/y = (-7/2)/(-33/2) = 7/33
Therefore, the required fraction is 7/33.
18. Find the value(s) of k so that the pair of equations x + 2y = 5 and 3x + ky + 15 = 0 has a unique solution. [CBSE 2019]
See SolutionFor a system of linear equations to have a unique solution, the ratio of coefficients must not be equal.
From the given equations:
x + 2y = 5 …(1)
3x + ky + 15 = 0 …(2)
Rearranging equation (2): 3x + ky = -15
For a unique solution, the ratio of coefficients must be unequal: 1/3 ≠ 2/k
This means k ≠ 6
Therefore, the value of k for which the system has a unique solution is any value except 6.
19. Sumit is 3 times as old as his son. Five years later, he shall be two and a half times as old as his son. How old is Sumit at present? [CBSE 2019]
See SolutionLet’s say Sumit’s present age is S years and his son’s present age is P years.
Given: S = 3P …(1)
S + 5 = 2.5(P + 5) …(2)
Substituting equation (1) into equation (2):
3P + 5 = 2.5(P + 5)
3P + 5 = 2.5P + 12.5
3P – 2.5P = 12.5 – 5
0.5P = 7.5
P = 15
Using equation (1): S = 3P = 3 × 15 = 45
Therefore, Sumit’s present age is 45 years.
20. For what value of k, will the following pair of equations have infinitely many solutions: 2x + 3y = 7 and (k + 2)x – 3(1 – k)y = 5k + 1 [CBSE 2019]
See SolutionFor a system of linear equations to have infinitely many solutions, the ratios of coefficients and constants must be equal.
Given equations: 2x + 3y = 7 …(1)
(k + 2)x – 3(1 – k)y = 5k + 1 …(2)
Simplifying equation (2): (k + 2)x – 3y + 3ky = 5k + 1
For infinitely many solutions: 2/(k + 2) = 3/(-3 + 3k) = 7/(5k + 1)
Looking at the first equality: 2/(k + 2) = 3/(-3 + 3k)
2(-3 + 3k) = 3(k + 2)
-6 + 6k = 3k + 6
3k = 12
k = 4
Let’s verify with the second equality: 3/(-3 + 3k) = 7/(5k + 1) With k = 4: 3/(-3 + 12) = 7/(20 + 1)
= 3/9 = 7/21 = 1/3
Therefore, k = 4 will give infinitely many solutions.
21. Find c, if the system of equations cx + 3y + (3 – c) = 0, 12x + cy – c = 0 has infinitely many solutions. [CBSE 2019]
See SolutionFor infinitely many solutions, the equations must be proportional.
Let’s rearrange the equations:
cx + 3y = c – 3 …(1)
12x + cy = c …(2)
For these to be proportional: c/12 = 3/c = (c-3)/c
From c/12 = 3/c:
c² = 36
c = ±6
From 3/c = (c-3)/c:
3 = c – 3
c = 6
Since both conditions must be satisfied, c = 6.
Therefore, c = 6 will give infinitely many solutions.
22. Find the relation between p and q, if x = 3 and y = 1 is the solution of the pair of equations x – 4y + p = 0 and 2x + y – q = 0 [CBSE 2019]
See SolutionSince (3, 1) is a solution to both equations, substituting these values:
From x – 4y + p = 0:
3 – 4(1) + p = 0
3 – 4 + p = 0
p = 1
From 2x + y – q = 0:
2(3) + 1 – q = 0
6 + 1 – q = 0
q = 7
Therefore, the relation between p and q is: p = 1 and q = 7.
Assertion-Reason Type Questions
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) Assertion is true but Reason is false.
(d) Assertion is false but Reason is false.
1. Assertion (A) The System of equations x – 3y – 5 = 0 and 2x – 7y + 11 = 0 has infinitely many solutions.
Reason (R) The system of equations a₁x + b₁y + c₁ = 0 and a₂x + b₂ y + c₂ = 0 has infinitely many solutions, when a₁/a₂ = b₁/b₂ = c₁/c₂
See SolutionCheck the ratios
a₁/a₂ = 1/2
b₁/b₂ = (-3)/(-7) = 3/7
c₁/c₂ = (-5)/11
Clearly:
a₁/a₂ ≠ b₁/b₂ ≠ c₁/c₂
So, the equations do not have infinitely many solutions.
They are intersecting lines, and thus have a unique solution.
Reason is TRUE (as a general condition for infinite solutions)
Assertion is FALSE.
Final Answer: (d) Assertion is false but Reason is true.
2. Assertion (A) If the pair of equations x + 2 y + 7 = 0, 3x + ky + 21 = 0 represents coincident lines, then the value of k is 6.
Reason (R) The pair of linear equations are coincident lines, if they have no solution.
See SolutionGiven System of Equations:
1) x + 2y + 7 = 0
→ a₁ = 1, b₁ = 2, c₁ = 7
2) 3x + ky + 21 = 0
→ a₂ = 3, b₂ = k, c₂ = 21
Condition for coincident lines:
A pair of linear equations represent coincident lines (i.e., infinitely many solutions) if: a₁/a₂ = b₁/b₂ = c₁/c₂
Substitute the values:
a₁/a₂ = 1/3
b₁/b₂ = 2/k
c₁/c₂ = 7/21 = 1/3
So set: 2/k = 1/3
⇒ k = 6
Therefore, Assertion is TRUE.
Evaluate Reason:
Reason says: “The pair of linear equations are coincident lines, if they have no solution.”
This is incorrect.
Coincident lines have infinitely many solutions.
No solution corresponds to parallel lines, not coincident ones.
Reason is FALSE.
Final Answer: (c) Assertion is true but Reason is false.
3. Assertion (A): The system of equations 2x + 4y = 10 and 3x + 6y = 12 is inconsistent.
Reason (R): A pair of linear equations which has no solution is called an inconsistent pair of linear equations.
See SolutionLet’s analyze the system of equations:
Equation 1: 2x + 4y = 10
Equation 2: 3x + 6y = 12
Dividing Equation 1 by 2: x + 2y = 5 Dividing Equation 2 by 3: x + 2y = 4
We now have x + 2y = 5 and x + 2y = 4, which are contradictory. Since the same expression (x + 2y) cannot equal both 5 and 4, the system has no solution.
Checking the ratios: a₁/a₂ = 2/3, b₁/b₂ = 4/6 = 2/3, c₁/c₂ = 10/12 = 5/6
Since a₁/a₂ = b₁/b₂ ≠ c₁/c₂, the system is inconsistent.
The Assertion is correct, and the Reason correctly defines an inconsistent system.
Answer: (a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
4. Assertion (A): 2x + 3y = 12 is a line which is parallel to 4x + 6y = 36.
Reason (R): The graph of linear equation ax = b, where a ≠ 0 is parallel to X-axis.
See SolutionLet’s analyze the equations:
Line 1: 2x + 3y = 12
Line 2: 4x + 6y = 36
Line 2 can be simplified by dividing by 2: 2x + 3y = 18
Comparing the two lines:
Line 1: 2x + 3y = 12
Line 2 (simplified): 2x + 3y = 18
These two lines have the same coefficients of x and y but different constants. Two lines with the same slope (−a/b) but different y-intercepts are parallel. So, the Assertion is true. However, the Reason states that the equation ax = b represents a line parallel to the X-axis. This is incorrect; a line parallel to the X-axis would be in the form y = k (a horizontal line), whereas ax = b represents a vertical line parallel to the Y-axis.
Answer: (c) Assertion is true but Reason is false.
5. Assertion (A): A two-digit number, where tens digit is greater than ones digit is obtained by either multiplying sum of the digits by 8 and adding 1 or by multiplying the difference of digits by 13 and adding 2. The number is 41.
Reason (R): The linear equations used are 7x – 2y + 1 = 0 and 14x – 3y – 2 = 0.
See SolutionLet’s say the two-digit number is 10x + y, where x is the tens digit and y is the ones digit. Given that x > y.
According to the first method: 10x + y = 8(x + y) + 1 10x + y = 8x + 8y + 1 2x – 7y = 1 7y – 2x = -1 … (1)
According to the second method: 10x + y = 13(x – y) + 2 10x + y = 13x – 13y + 2 10x + y – 13x + 13y – 2 = 0 -3x + 14y – 2 = 0 3x – 14y + 2 = 0 … (2)
Multiplying equation (1) by 3: 21y – 6x = -3 … (3)
From equations (2) and (3): 3x – 14y + 2 = 0 -6x + 21y = -3 -3x + 7y = -1
Subtracting: -3x + 7y – (-3x + 14y) = -1 – 2 -7y = -3 y = 3/7 (not an integer)
This system doesn’t yield the number 41, so either the Assertion or our approach is incorrect.
Let’s check if 41 satisfies the conditions: 41 = 4×10 + 1 Sum of digits = 4 + 1 = 5 8(5) + 1 = 41 ✓ Difference of digits = 4 – 1 = 3 13(3) + 2 = 41 ✓
The number 41 does satisfy the given conditions. However, the equations in the Reason (7x – 2y + 1 = 0 and 14x – 3y – 2 = 0) don’t match our derived equations.
Answer: (c) Assertion is true but Reason is false.
6. Assertion (A): The number of common solutions for the system of linear equations 5x + 4y + 6 = 0 and 10x + 8y = 12 is zero.
Reason (R): The system of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 has a unique solution, if a₁/a₂ = b₁/b₂.
See SolutionLet’s analyze the system:
Equation 1: 5x + 4y + 6 = 0 or 5x + 4y = -6
Equation 2: 10x + 8y = 12
Dividing Equation 2 by 2: 5x + 4y = 6
We now have: 5x + 4y = -6 (from Equation 1) 5x + 4y = 6 (from Equation 2)
These are contradictory since the same expression cannot equal both -6 and 6. Hence, the system has no common solution (zero solutions).
Checking the ratios: a₁/a₂ = 5/10 = 1/2, b₁/b₂ = 4/8 = 1/2, c₁/c₂ = -6/12 = -1/2
Since a₁/a₂ = b₁/b₂ ≠ c₁/c₂, the system is inconsistent, confirming zero solutions.
However, the Reason is incorrect. A system has a unique solution when a₁/a₂ ≠ b₁/b₂. If a₁/a₂ = b₁/b₂ = c₁/c₂, the system has infinitely many solutions, and if a₁/a₂ = b₁/b₂ ≠ c₁/c₂, the system has no solution.
Answer: (c) Assertion is true but Reason is false.
7. Assertion (A): If the equations 3x – y + 8 = 0 and 6x – ky = -16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is 5/6.
See SolutionFor two lines to be coincident, they must have: a₁/a₂ = b₁/b₂ = c₁/c₂
For our system:
Line 1: 3x – y + 8 = 0 or 3x – y = -8
Line 2: 6x – ky = -16
For these to be coincident: 3/6 = -1/(-k) = -8/(-16) 1/2 = 1/k = 1/2
This gives k = 2, confirming the Assertion.
The Reason deals with a different system. For parallel lines: a₁/a₂ = b₁/b₂ ≠ c₁/c₂
For 3x + 2ky = 2 and 2x + 5y + 1 = 0: 3/2 = 2k/5 3×5 = 2×2k 15 = 4k k = 15/4 = 3.75, not 5/6
Answer: (c) Assertion is true but Reason is false.
8. Assertion (A): x = 2, y = 1 is a solution of pair of equations 3x – 2y = 4 and 2x + y = 5.
Reason (R): A pair of values (x, y) satisfying each one of the equations in a given system of two simultaneous linear equations in x only is called a solution of the system of equations.
See SolutionLet’s check if (2, 1) satisfies both equations:
For 3x – 2y = 4: 3(2) – 2(1) = 6 – 2 = 4 ✓
For 2x + y = 5: 2(2) + 1 = 4 + 1 = 5 ✓
So (2, 1) is indeed a solution of the given system.
The Reason, however, contains an error. A solution of a system of linear equations must satisfy all equations in the system simultaneously, not just “each one” separately. Also, the Reason mentions “equations in x only” which is incorrect for a system in x and y.
Answer: (c) Assertion is true but Reason is false.
9. Assertion (A): Graphically, the pair of linear equations 2x – y – 5 = 0 and x – y – 3 = 0 represents intersecting lines.
Reason (R): The linear equations 2x – y – 5 = 0 and x – y – 3 = 0 meet the Y-axis at (0, 3) and (0, -5), respectively.
See SolutionThe two equations represent:
Line 1: 2x – y – 5 = 0 or y = 2x – 5
Line 2: x – y – 3 = 0 or y = x – 3
These have different slopes (2 and 1), so they will intersect. The Assertion is true.
To check where these lines meet the Y-axis:
For Line 1, when x = 0: y = 2(0) – 5 = -5
For Line 2, when x = 0: y = 0 – 3 = -3
So Line 1 meets the Y-axis at (0, -5) and Line 2 at (0, -3), not at (0, 3) as stated in the Reason.
Answer: (c) Assertion is true but Reason is false.
10. Assertion (A): If 4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750, then the cost of 1 chair is ₹ 150.
Reason (R): Sum of the ages of a mother and her daughter is 40 yr. If mother’s age is 3 times that of her daughter, then the daughter’s age is 12 yr.
See SolutionLet’s solve the system:
4 chairs and 3 tables cost ₹2100: 4x + 3y = 2100
5 chairs and 2 tables cost ₹1750: 5x + 2y = 1750
Multiplying the first equation by 5: 20x + 15y = 10500 Multiplying the second equation by 4: 20x + 8y = 7000 Subtracting: 7y = 3500 y = 500 (cost of one table)
Substituting back to find x: 4x + 3(500) = 2100 4x + 1500 = 2100 4x = 600 x = 150 (cost of one chair)
The Assertion is correct.
The Reason presents an unrelated problem. Let’s solve it to verify: Mother’s age = m, Daughter’s age = d m + d = 40 m = 3d Substituting: 3d + d = 40 4d = 40 d = 10
This gives the daughter’s age as 10 years, not 12 years as stated in the Reason.
Answer: (c) Assertion is true but Reason is false.
11. Assertion (A): The pair of linear equations has a unique solution. x – 2y + 3 = 0 3x + 4y – 11 = 0
Reason (R): The pair of linear equations represents a pair of coincident lines. (CBSE )
See SolutionTo determine the nature of the system, we check:
a₁/a₂ = 1/3, b₁/b₂ = -2/4 = -1/2
Since a₁/a₂ ≠ b₁/b₂, the lines will intersect at exactly one point, giving a unique solution.
However, coincident lines would have a₁/a₂ = b₁/b₂ = c₁/c₂ and would provide infinitely many solutions, not a unique solution.
Answer: (c) Assertion is true but Reason is false.
Case Based Type Questions
Case Study 1
Case 1. A coaching institute of Mathematics conducts classes in two batches I and II and rich and poor children are different. In batch I, there are 20 poor and 5 rich children, whereas in batch II, there are 5 poor and 25 rich children. The total monthly collection of fees from batch I is ₹ 9000 and from batch II is ₹ 26000. Assume that each poor child pays ₹ x per month and each rich child pays ₹ y per month.
(i). Represent the information given above in terms of x and y.
See SolutionFrom Batch I: 20x + 5y = 9000 From Batch II: 5x + 25y = 26000
(ii). Find the monthly fee paid by a poor child. Or Find the difference in the monthly fee paid by a poor child and a rich child.
See SolutionTo find x (fee paid by a poor child): From Batch I: 20x + 5y = 9000 … (1) From Batch II: 5x + 25y = 26000 … (2)
Multiplying equation (1) by 1 and equation (2) by 4: 20x + 5y = 9000 20x + 100y = 104000
Subtracting: -95y = -95000 y = 1000 (fee paid by a rich child)
Substituting back in equation (1): 20x + 5(1000) = 9000 20x + 5000 = 9000 20x = 4000 x = 200 (fee paid by a poor child)
The monthly fee paid by a poor child is ₹200.
The difference in fees: y – x = 1000 – 200 = ₹800
(iii). If there are 10 poor and 20 rich children in batch II, what is the total
monthly collection of fees from batch II?
See SolutionWith 10 poor and 20 rich children, the total collection would be: 10x + 20y = 10(200) + 20(1000) = 2000 + 20000 = ₹22000
Therefore, the total monthly collection from batch II with this new composition would be ₹22000.
Class 10 Mathematics NCERT Chapter 3 exercise solutions provide step-by-step explanations, ensuring that students grasp the concepts of substitution, elimination and cross-multiplication methods. With detailed NCERT 10th Math Chapter 3 solutions PDF, learners can easily access practice questions and solved examples for better preparation. Practice Questions with Solutions based on Class 10 Maths Chapter 3:
1. A pair of linear equations is shown below, where b is an integer.
2x – y = b + 1
x + (b – 1)y = 3b
For any given value of b, how many solutions does this pair of equations have? Justify your answer.
See SolutionGiven equations:
2x – y = b + 1
x + (b – 1)y = 3b
To solve this, we’ll check if the equations are consistent and determine if they have a unique solution, infinite solutions, or no solution.
Rearranging the first equation:
y = 2x – b – 1 Substituting into the second equation:
x + (b – 1)(2x – b – 1) = 3b
x + (b – 1)(2x) – (b – 1)(b + 1) = 3b
x + 2(b – 1)x – (b – 1)(b + 1) = 3b
x + 2bx – 2x – b² – 1 + b = 3b
x + 2bx – 2x – b² – 1 + b = 3b
2bx – x – b² – 1 + b = 3b
2bx – x = 3b + b² + 1 – b
(2b – 1)x = 3b + b² + 1 – b
(2b – 1)x = b² + 2b + 1
(2b – 1)x = (b + 1)²
If 2b – 1 ≠ 0 (i.e., b ≠ 1/2), then x = (b + 1)²/(2b – 1), which gives a unique solution.
If b = 1/2, then 2b – 1 = 0 and we get 0 = (b + 1)² = (3/2)² = 9/4, which is a contradiction.
Therefore, for any value of b, there is exactly one solution to this system of equations.
2. Different shades of purple are obtained by mixing different quantities of red and blue colours. An artist combined 5 L of red paint with 7 L of blue paint to achieve a shade of purple, incurring a cost of ₹5000. To achieve a different shade of purple, she mixed 7 L of red paint and 5 L of blue paint, incurring a cost of ₹4600. Calculate the price of red and blue paint per litre.
See SolutionGiven: Mixture 1: 5L red + 7L blue = 12L purple at cost ₹5000
Mixture 2: 7L red + 5L
blue = 12L
Purple at cost ₹4600
Let r = price of red paint per liter Let b = price of blue paint per liter
We can write two equations:
5r + 7b = 5000
7r + 5b = 4600
Multiplying the first equation by 7 and the second by 5:
35r + 49b = 35000
35r + 25b = 23000
Subtracting the second from the first:
24b = 12000
b = 500
Substituting back into the first equation:
5r + 7(500) = 5000
5r + 3500 = 5000
5r = 1500
r = 300
Therefore, red paint costs ₹300 per liter and blue paint costs ₹500 per liter.
3. In a chemistry lab, scientists are studying a chemical reaction between two substances, Substance A and Substance B.
The following was known : The total mass of the substances before the reaction was 9 gm.
The difference in mass between Substances A and B before the reaction was 6 gm.
Determine the mass of Substances A and B before the reaction. Show your work.
See SolutionGiven: Total mass before reaction = 9 gm
Difference in mass between substances A and B = 6 gm
Let a = mass of substance A Let b = mass of substance B
We can write two equations:
a + b = 9
a – b = 6
Solving these equations:
a + b = 9
a – b = 6
We get: 2a = 15
a = 7.5
Substituting back:
7.5 + b = 9
b = 1.5
Therefore, the mass of substance A before the reaction was 7.5 gm, and the mass of substance B before the reaction was 1.5 gm.
4. A two-digit number is such that the sum of its digits is 11. When the digits are reversed, the resulting number increases by 27. Determine the original two-digit number. Show your work.
See SolutionLet’s denote the tens digit as x and the units digit as y. The original number = 10x + y The reversed number = 10y + x
Given information:
Sum of digits: x + y = 11
When digits are reversed, the number increases by 27: 10y + x = (10x + y) + 27
Let’s solve these equations:
10y + x = 10
x + y + 27
10y – y = 10x – x + 27
9y = 9x + 27
y = x + 3
Substituting this into
x + y = 11:
x + (x + 3) = 11
2x + 3 = 11
2x = 8 x = 4
So y = x + 3 = 4 + 3 = 7
Therefore, the original two-digit number is 47.
Let’s verify:
Sum of digits: 4 + 7 = 11
Reversed number: 74
Difference: 74 – 47 = 27
NCERT Class 10 Maths Chapter 3 Exercises textbook solutions cover all exercises, offering clarity on complex problems. For those aiming to improve, referring to Class 10 NCERT Maths Chapter 3 important questions and Class 10 Math 3rd chapter solved problems can boost confidence and improve exam performance.
Class 10 Maths Chapter 3 Solutions for Board Exams
To perform well in mathematics, students can download the NCERT Class 10 Maths Chapter 3 solutions PDF and practice regularly. These materials not only provide Class 10 Math Chapter 3 question answers but also explain concepts in an easy-to-follow manner. NCERT Book Class 10 Maths Chapter 3 detailed solutions and Class 10 Mathematics Chapter 3 Exercises solution manual serve as perfect companions for exam preparation, ensuring a thorough understanding of solving linear equations.
Students can explore 10th NCERT Maths Chapter 3 practice questions and NCERT Class 10 Math Book Chapter 3 solved exercises to reinforce their learning. For additional guidance, the Class 10 Maths Chapter 3 solution guide and free-to-download Class 10 Maths Chapter 3 solution book are invaluable resources. Accessing these CBSE Class 10 Mathematics Chapter 3 solutions online makes preparation hassle-free and efficient for every aspiring student.
Class 10 Maths Chapter 3 Solutions for State Boards
Class 10th Maths Chapter 3 Solutions
Key Highlights of Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
Class 10 Maths Chapter 3 focuses on solving pairs of linear equations using substitution, elimination and cross-multiplication methods. Key points include graphical solutions, consistency conditions and practical problem-solving applications. Understanding these methods, practicing solved examples and mastering important questions are crucial for scoring well in board exams.
| Day | Topics to Cover | Practice/Activities | Outcome |
|---|---|---|---|
| Day 1 | Introduction to Linear Equations | Understand the basics and solve 5 simple equations | Familiarity with the concept of linear equations |
| Day 2 | Graphical Representation of Equations | Plot 5 pairs of linear equations on a graph | Understanding graphical solutions |
| Day 3 | Substitution Method | Practice 10 questions using substitution | Mastery of substitution technique |
| Day 4 | Elimination Method | Practice 10 questions using elimination | Mastery of elimination technique |
| Day 5 | Cross-Multiplication Method | Solve 10 equations using cross-multiplication | Proficiency in cross-multiplication |
| Day 6 | Practical Applications | Solve 5 word problems from NCERT | Understanding real-life applications |
| Day 7 | Revision | Review notes, solve sample papers | Confidence and readiness for exams |
| Class: 10 | Mathematics |
| Chapter 3: | Pair of Linear Equations in Two Variables |
| Number of Exercises: | 3 (Three) |
| Content: | Textbook Exercises Solutions |
| Session: | Academic Year 2025-26 |
| Medium: | English and Hindi Medium |
According to new syllabus the class 10th math has only three exercise for board exams. Exercise 3.1 is deleted now. The exercise 3.2 become ex. 3.1, Exercise 3.3 become ex. 3.2 and exercise 3.4 become ex. 3.3 now. The split up syllabus for 10th mathematics chapter 3 is as follows:
Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency.
Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically – by substitution, by elimination. Simple situational problems.
- Now, Number of exercise: 3
- Number of Period needed: 15
- Weightage of the Chapter: 7-8
NCERT class 10 Maths chapter 3 Solutions
UP Board students of High School are now using NCERT Textbooks for most of the subjects. Class 10 Mathematics Books for UP Board is same as Books for Class 10 Math in CBSE Board. So, the students of Uttar Pradesh Board can download, UP Board Solutions for class 10 Math Chapter 3 from this page of Tiwari Academy. Solutions are available in Hindi and English Medium. Graphs are given for all the questions if required. Visit to Discussion Forum to ask your questions. You can reply the questions already asked by other users.
NCERT 10th Maths Chapter 3 Solutions
In NCERT Solutions Class 10, all exercises are solved in both English as well as in Hindi medium in order to help all type of students for new academic session. In Maths 10, Exercise 3.1, 3.2, and 3.3 solutions, if there is any inconvenient to understand, please inform us, we will try to solve it. All NCERT Solutions are made for the CBSE exam for March, based on latest CBSE Syllabus 2025-26.
Changes in CBSE Syllabus for Class 10 Maths Chapter 3
CBSE has reduced the syllabus of all subjects in all the classes. The CBSE Syllabus for Class 10 Maths is reduced to 65 percent now. The changes in 10th Maths chapter 3: Linear equations in two variables are given below.
The new CBSE Syllabus for 2025-26 Class 10 Maths Chapter 3
Pair of linear equations in two variables and graphical method of their solution, consistency /inconsistency.
Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically – by substitution, by elimination. Simple situational problems. Simple problems on equations reducible to linear equations.
Deleted Section from previous Syllabus
Solution of a pair of linear equations in two variables by Cross-multiplication.
Previous Years Questions – 1 Mark or 2 Marks
- Find whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident: 3x + y = 7 & 6x + 2y = 8. [CBSE 2016]
- Find the value of k for which the system of equations 3𝑥 − 4𝑦 = 7; 𝑘𝑥 + 3𝑦 − 5 = 0 has no solution. [CBSE 2014]
- A father is three times as old as his son. After five years, his age will be two and a half times as old as his son. Represent this situation algebraically only. [CBSE 2013]
- For which value of p does the pair of equations given below have a unique solutions? 4x + py + 8 = 0; 2x + 2y + 2 = 0. [CBSE 2010, 2011, 2013]
- For what value of k, the following system of linear equations has no solutions? 3x + y = 1; (2k – 1)x + (k – 1)y =2k + 1. [CBSE 2010, 2011, 2012]
Previous Years Questions – 3 Marks
- Solve for x and y: 11/x – 1/y = 10 & 9/x – 4/y = 5. [CBSE 2016]
- Solve using cross multiplication method: 5x + 4y – 4 = 0 & x – 12y – 20 = 0. [CBSE 2016]
- A man has certain notes of denomination ₹ 20 and ₹ 5 which amount to ₹380. If the number of notes of each kind are interchanged, they amount to ₹60 less than before. Find the number of notes of each denomination. [CBSE 2015]
- Find the value of ‘k’ for which the following system of equations represents a pair of coincident lines: 𝑥 + 2𝑦 = 3; (𝑘 − 1)𝑥 + (𝑘 + 1)𝑦 = 𝑘 + 3. [CBSE 2014]
- Check graphically, whether the pair of equations x + 3y = 6 & 2x – 3y = 12 is consistent. If so, then solve them graphically. [CBSE 2013]
- The path of a train A is given by the equation x + 2y – 4 = 0 and path of another train B is given by the equation 2x + 4y – 12 = 0. Represent this situation graphically and find whether the two trains meet each other at some place. [CBSE 2013]
- Form a pair of linear equations in two variables from the data given and solve it graphically: Tina went to a book shop to get some story books and textbooks. When her friends asked her how many of each she had bought, she answered – ‘The number of textbooks is two more than twice the number of story books bought. Also, the number of textbooks is four less than four times the number of story books bought. Help her friends to find the number of textbooks and story books she had bought. [CBSE 2013]
- Determine graphically, the coordinates of the vertices of a triangle whose sides are graphs of the equations 2x – 3y + 6 = 0, 2x + 3y – 18 = 0 and y – 2 = 0. Also, find the area of this triangle. [CBSE 2010, 2011]
Previous Years Questions – 4 Marks
- For Uttarakhand flood victims’ two sections A and B of class X contributed ₹ 1500. If the contribution of X A was ₹ 100 less than that of X B, find graphically the amounts contributed by both the sections. [CBSE 2016]
- Three lines 3x + 5y = 15, 6x – 5y = 30 and x = 0 are enclosing a beautiful triangular park. Find the points of intersection of the lines graphically and the area of the park if all measurements are in km. [CBSE 2016]
- Some people collected money to be donated in two Old Age Homes. A part of the donation is fixed and remaining depends on the number of old people in the home. If they donated ₹ 14500 in the home having 60 people and ₹ 19500 with 85 people, find the fixed part of donation and the amount donated for each people. What is the inspiration behind this? [CBSE 2016]
- While teaching about the Indian National flag, teacher asked the students that how many lines are there in Blue colour wheel? One student replies that it is 8 times the number of colours in the flag. While other says that the sum of the number colours in the flag and number of lines in the wheel of the flag is 27. Convert the statements given by the students into linear equation of two variables. Find the number of lines in the wheel. [CBSE 2015]
- Determine the value of k for which the following system of linear equations has infinite number of solutions: (k – 3)x + 3y = k & kx + ky = 12. [CBSE 2015]
- Draw the graph of the following pair of linear equation: x + 3y = 6 & 2x – 3y = 12. Find the ratio of the areas of the two triangles formed by first line, x = 0, y = 0 and second line, x = 0, y = 0. [CBSE 2015]
- Places A and B are 200km apart on a high way. One car starts from A and another from B at the same time. If the cars travel in the same directions at different speeds, they meet in 10 hours. Find the speeds of the two cars. [CBSE 2014]
- Show graphically that the system of equations𝑥 + 2𝑦 = 4 and 7𝑥 + 4𝑦 = 18 is consistent with a unique solution (2, 1). [CBSE 2014]
10th Maths Chapter 3 Questions for Practice
- 1. Solve for x and y: 99x + 101y = 1499; 101x + 99y = 1501. [CBSE 2010, 2011, 2012, 2013, 2014]
- 2. The age of father is equal to sum of ages of his 4 children. After 30 years, sum of the ages of the children will be twice the age of the father. Find the age of the father. [CBSE 2013]
- 3. A person can row a boat 8 km upstream and 24 km downstream in 4 hours. He can row 12 km downstream and 12 km upstream in 4 hours. Find the speed of rowing in still water and the speed of the current. [CBSE 2013]
- 4. Solve for x and y: 37x + 43y = 123; 43x + 37y = 117. [CBSE 2010, 2011, 2012]
- 5. Draw the graph of the equations: x – y + 1 = 0 & 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x – axis and shade the triangular region. Also calculate the area of the triangle so formed. [CBSE 2011]
- 6. The sum of a 2 digit number and number obtained by reversing the order of digits is 99. If the digits of the number differ by 3, find the number. [CBSE 2011]
- 7. Check graphically whether the pair of linear equations 4x – y – 8 = 0 and 2x – 3y + 6 = 0 is consistent. Also determine the vertices of the triangle form by these lines and x – axis. [CBSE 2006, 2011]
- 8. The sum of the digits of a two digit number is 9. Nine times this number is twice the number obtained by reversing the digits. Find the number. [CBSE 2010]
- 9. A leading library has a fixed charge for the first three days and an additional charge for each day thereafter. Sarita paid ₹ 27 for a book kept for seven days. While Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day. [CBSE 2010]
- 10. Solve the following system of linear equations by elimination method: 6(ax + by) = 2a + 2b and 6(bx – ay) = 3b – 2a. [CBSE 2006, 2004]
Practice and Revision of One Mark Type Question Answers with solution and Explanation.
1. For the pair of equations to have infinitely many solutions, what is the relationship between the coefficients?
See AnswerThe ratio of corresponding coefficients must be equal:
a₁/a₂ = b₁/b₂ = c₁/c₂.
2. If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find the value of k.
See AnswerFor parallel lines, a₁/a₂ = b₁/b₂.
So, 3/2 = 2k/5.
This gives 4k = 15
⇒ k = 15/4.
3. Do the equations x + 2y – 8 = 0 and 2x + 4y = 16 represent a pair of coincident lines?
See AnswerYes.
The second equation can be written as 2x + 4y – 16 = 0.
Here a₁/a₂ = 1/2, b₁/b₂ = 2/4 = 1/2, and c₁/c₂ = -8/-16 = 1/2.
The condition for coincident lines is met.
4. A boat goes 10 km upstream in 5 hours. Write a linear equation representing this situation if the speed of the boat in still water is x km/hr and the speed of the stream is y km/hr.
See AnswerSpeed upstream is (x – y) km/hr.
Since distance = speed × time
Therefore, the equation is 10 = (x – y) × 5, which simplifies to x – y = 2.
5. Is the pair of linear equations 2x + 3y = 5 and 4x + 6y = 15 consistent or inconsistent?
See AnswerInconsistent.
Here a₁/a₂ = 2/4 = 1/2, b₁/b₂ = 3/6 = 1/2, and c₁/c₂ = 5/15 = 1/3.
Since a₁/a₂ = b₁/b₂ ≠ c₁/c₂, the lines are parallel and have no solution.
6. What is the number of solutions for the pair of equations x = 5 and y = 5?
See AnswerOne unique solution, which is (5, 5).
7. If we solve the equations x + 2y = 10 and y = 3, what is the value of x?
See AnswerSubstitute y = 3 into the first equation:
x + 2(3) = 10
⇒ x + 6 = 10, which gives x = 4.
8. Form a linear equation in two variables for the statement: “The cost of a notebook is twice the cost of a pen.”
See AnswerLet the cost of a notebook be x and the cost of a pen be y.
The equation is x = 2y or x – 2y = 0.
9. Write another linear equation in two variables such that it forms intersecting lines with the equation 2x + 3y – 8 = 0.
See AnswerAny equation where the ratio a₁/a₂ ≠ b₁/b₂.
For example, 3x + 2y – 7 = 0.
10. What is the condition for a pair of linear equations to be dependent?
See AnswerA pair of linear equations is dependent if it has infinitely many solutions, which occurs when the lines are coincident (a₁/a₂ = b₁/b₂ = c₁/c₂).
11. Find the value of x and y from the equations x – y = 3 and x + y = 7.
See AnswerAdding the two equations, we get 2x = 10, so x = 5.
Substituting x = 5 gives y = 2.
12. The sum of two numbers is 35 and their difference is 13. Form the pair of linear equations.
See AnswerLet the numbers be x and y.
The equations are x + y = 35 and x – y = 13.
13. For the equation 4x + 5y = 20, find the point where the line intersects the x-axis.
See AnswerOn the x-axis, y = 0.
So, 4x + 5(0) = 20, which gives 4x = 20 or x = 5.
The point is (5, 0).
14. How many solutions does a dependent pair of linear equations have?
See AnswerInfinitely many solutions.
15. If 3x + y = 10, express y in terms of x.
See Answery = 10 – 3x.
Practice and Revision of Two or Three Marks Type Question Answers with solution and Explanation.
1. Solve the following pair of linear equations by the substitution method:
7x – 15y = 2
x + 2y = 3
See AnswerFrom the second equation, x = 3 – 2y.
Substitute this into the first equation:
7(3 – 2y) – 15y = 2
⇒ 21 – 14y – 15y = 2
⇒ 21 – 29y = 2
⇒ -29y = -19
⇒ y = 19/29.
Now, substitute y back:
x = 3 – 2(19/29) = 3 – 38/29 = (87 – 38)/29 = 49/29.
Hence, x = 49/29, y = 19/29.
2. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
See AnswerLet length be l and width be w.
Given: l = w + 4 (Equation 1)
Perimeter = 2(l + w).
Half the perimeter is l + w.
Given: l + w = 36 (Equation 2)
Substitute (1) into (2):
(w + 4) + w = 36
⇒ 2w + 4 = 36
⇒ 2w = 32
⇒ w = 16 m.
Then, l = 16 + 4 = 20 m.
Dimensions are Length = 20 m, Width = 16 m.
3. Find the value of k for which the pair of linear equations kx + 3y – (k – 3) = 0 and 12x + ky – k = 0 has infinitely many solutions.
See AnswerFor infinitely many solutions: a₁/a₂ = b₁/b₂ = c₁/c₂.
k/12 = 3/k = -(k – 3)/-k
From k/12 = 3/k, we get k² = 36, so k = 6 or k = -6.
From 3/k = (k – 3)/k, we get 3k = k(k – 3).
Since k cannot be 0, we divide by k to get 3 = k-3 so k = 6.
Hence, k = 6.
4. Solve the pair of equations using the elimination method:
2x + 3y = 11
2x – 4y = -24
See AnswerSubtract the second equation from the first:
(2x + 3y) – (2x – 4y) = 11 – (-24)
⇒ 7y = 35
⇒ y = 5
Substitute y = 5 in the first equation:
2x + 3(5) = 11
⇒ 2x + 15 = 11
⇒ 2x = -4
⇒ x = -2.
Hence, x = -2, y = 5.
5. Determine the point of intersection of the lines represented by 3x + 2y = 12 and x – y = 1.
See AnswerFrom the second equation, x = 1 + y.
Substitute in the first: 3(1 + y) + 2y = 12
3 + 3y + 2y = 12
5y = 9, so y = 9/5.
Then x = 1 + 9/5 = 14/5.
Point of intersection: (14/5, 9/5).
6. Find the area of the triangle formed by the lines x = 0, y = 0 and x + y = 4.
See AnswerThe lines intersect the axes at (4, 0) and (0, 4).
The triangle formed has vertices at (0,0), (4,0) and (0,4).
Area = 1/2 × base × height
= 1/2 × 4 × 4
= 8 square units.
7. Write whether the pair of equations 4x – 5y = 7 and 20x – 25y = 35 are consistent or not.
See AnswerHere: a₁/a₂ = 4/20 = 1/5
b₁/b₂ = -5/-25 = 1/5 and
c₁/c₂ = 7/35 = 1/5.
Since a₁/a₂ = b₁/b₂ = c₁/c₂, the lines are coincident and have infinitely many solutions.
Therefore, the pair is consistent and dependent.
8. For the equations x + y = 4 and x – y = 2, find the point of intersection.
See AnswerAdd the equations: (x + y) + (x – y) = 4 + 2
⇒ 2x = 6
⇒ x = 3.
Substitute in x + y = 4
⇒ 3 + y = 4
⇒ y = 1.
Point of intersection: (3, 1).
9. Two numbers are in the ratio 5:3. If the sum of the numbers is 56, find the numbers.
See AnswerLet the numbers be 5x and 3x.
Then, 5x + 3x = 56
⇒ 8x = 56
⇒ x = 7.
Therefore, the numbers are 35 and 21.
10. Solve the pair of equations 3x + y = 12 and x – y = 2 by the substitution method.
See AnswerFrom the second equation, x = 2 + y.
Substitute in the first: 3(2 + y) + y = 12
⇒ 6 + 3y + y = 12
⇒ 4y = 6
⇒ y = 1.5
Then x = 2 + 1.5 = 3.5
Hence, x = 3.5, y = 1.5.
Practice and Revision of Three or Four Marks Type Question Answers with solution and Explanation.
1. Solve the following pair of equations by the elimination method:
5x – 2y = 4
3x + 4y = 20
See AnswerMultiply the first equation by 2 to make the coefficients of y equal:
(5x – 2y = 4) × 2 ⇒ 10x – 4y = 8
(3x + 4y = 20)
Add both equations:
(10x + 3x) + (-4y + 4y) = 8 + 20
⇒ 13x = 28
⇒ x = 28/13
Substitute in 5x – 2y = 4:
⇒ 5(28/13) – 2y = 4
⇒ 140/13 – 2y = 4
Multiply by 13:
140 – 26y = 52
⇒ -26y = -88
⇒ y = 88/26 = 44/13
Hence: x = 28/13, y = 44/13
2. A fraction becomes 1/3 when 2 is subtracted from the numerator and 2 is added to the denominator. If 4 is added to the numerator and 3 is subtracted from the denominator, it becomes 3/2. Find the fraction.
See AnswerLet the fraction be x/y.
According to the question:
(x – 2)/(y + 2) = 1/3
⇒ 3x – 6 = y + 2
⇒ 3x – y = 8 …(i)
(x + 4)/(y – 3) = 3/2
⇒ 2x + 8 = 3y – 9
⇒ 2x – 3y = -17 …(ii)
Multiply (i) by 3:
9x – 3y = 24 …(iii)
Subtract (ii) from (iii):
(9x – 3y) – (2x – 3y) = 24 – (-17)
⇒ 7x = 41
⇒ x = 41/7
Substitute x = 41/7 in (i):
3(41/7) – y = 8
⇒ 123/7 – y = 8
⇒ y = 123/7 – 56/7 = 67/7
Fraction = x/y = (41/7) ÷ (67/7) = 41/67
3. Solve the equations using the cross-multiplication method:
2x – 3y + 8 = 0
x + 2y – 3 = 0
See AnswerFormula:
x/(b₁c₂ – b₂c₁) = y/(c₁a₂ – c₂a₁) = 1/(a₁b₂ – a₂b₁)
Substitute:
a₁ = 2, b₁ = -3, c₁ = 8
a₂ = 1, b₂ = 2, c₂ = -3
Therefore:
b₁c₂ – b₂c₁ = (-3)(-3) – (2)(8) = 9 – 16 = -7
c₁a₂ – c₂a₁ = (8)(1) – (-3)(2) = 8 + 6 = 14
a₁b₂ – a₂b₁ = (2)(2) – (1)(-3) = 4 + 3 = 7
So,
x/(-7) = y/14 = 1/7
From x/(-7) = 1/7 ⇒ x = -1
From y/14 = 1/7 ⇒ y = 2
Hence: x = -1, y = 2
4. A motorboat, whose speed is 18 km/h in still water, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
See AnswerLet the speed of the stream be x km/h.
Speed upstream = (18 – x)
Speed downstream = (18 + x)
Given:
24/(18 – x) = 24/(18 + x) + 1
Multiply both sides by (18 – x)(18 + x):
24(18 + x) = 24(18 – x) + (18 – x)(18 + x)
⇒ 432 + 24x = 432 – 24x + (324 – x²)
⇒ 432 + 24x = 756 – 24x – x²
⇒ x² + 48x – 324 = 0
Using the quadratic formula:
x = [-48 ± √(48² – 4(1)(-324))]/2
x = [-48 ± √(2304 + 1296)]/2
x = [-48 ± √3600]/2
x = [-48 ± 60]/2
x₁ = (12)/2 = 6, x₂ = (-108)/2 = -54
Rejecting negative value.
x = 6 km/h
Speed of the stream = 6 km/h
5. The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits differ by 2, find the number.
See AnswerLet the tens digit be x and the units digit be y.
Then, the number = 10x + y.
Reversed number = 10y + x.
Equation (1): (10x + y) + (10y + x) = 66
⇒ 11x + 11y = 66
⇒ x + y = 6 …(i)
Equation (2): x – y = 2 …(ii)
Adding (i) and (ii):
2x = 8
⇒ x = 4
Substitute in (i):
4 + y = 6
⇒ y = 2
Hence, the number = 10(4) + 2 = 42
Historical Facts!
History about Linear Equations with two variables. Around 4000 years ago, Babylon knew how to solve a simple linear equation with two variables. Around 200 BC, the Chinese published that “Nine Chapters of the Mathematical Art”, they displayed the ability to solve a system of equations in three variables (Perotti).
Evidence from about 300 BC indicates that the Egyptians also knew how to solve problems involving a system of two equations in two unknown quantities, including quadratic equations.
Euler brought to light the idea that a system of equations doesn’t necessarily have to have a solution (Perotti). He recognized the need for conditions to be placed upon unknown variables in order to find a solution.
With the turn into the 19th century Gauss introduced a procedure to be used for solving a system of linear equations. Cayley, Euler, Sylvester and others changed linear systems into the use of matrices to represent them. Gauss brought his theory to solve systems of equations proving to be the most effective basis for solving unknowns.
What topics are covered in NCERT Solutions for Class 10 Maths Chapter 3?
NCERT Textbook Solutions for Class 10 Maths Chapter 3 focus on solving pairs of linear equations in two variables using various methods like substitution, elimination and cross-multiplication. It also covers graphical representation and interpretation of solutions. The solutions provide step-by-step explanations for all exercise problems, ensuring that students develop a clear understanding of the concepts. The chapter 3 of 10th Maths, emphasizes real-life applications of linear equations, which helps students relate the mathematical concepts to practical scenarios. By practicing these solutions, students can strengthen their foundation for competitive exams and Class 10 board examinations.
How many exercises are there in Class 10 Maths chapter 3?
There are in all 7 exercises in class 10 mathematics chapter 3 (Pair of linear equations in two variables).
- In second exercise (Ex 3.1), there are in all 7 questions.
- In third exercise (Ex 3.2), there are in all 3 questions.
- In fourth exercise (Ex 3.3), there are only 2 questions.
- So, there are total 12 questions in class 10 mathematics chapter 3 (Pair of linear equations in two variables).
- In chapter 3 of 10th Maths there are in all good examples. Examples 4, 5, 6 are based on Ex 3.1, Examples 7, 8, 9, 10 are based on Ex 3.2, Examples 11, 12, 13 are based on Ex 3.3.
Where can I find NCERT Class 10 Maths Chapter 3 solutions online?
You can find reliable NCERT Class 10 Maths Chapter 3 solutions online on various educational websites and apps. These platforms offer detailed step-by-step explanations for each exercise question, along with additional resources like solved examples and important questions. Many websites also provide free downloadable PDFs, which can be accessed anytime for offline study. These solutions are curated by subject experts, ensuring accuracy and alignment with the NCERT syllabus. By accessing these online resources, students can enhance their learning experience, clarify doubts and improve their problem-solving skills effectively.
What are the most important questions of 10th Maths Chapter 3?
- In second exercise (Ex 3.1), all questions are important.
- In third exercise (Ex 3.2), Q1 (iv, v, vi), 2, 3 are important.
- In fourth exercise (Ex 3.3), Q2 is important.
- Important examples of chapter 3 (Pair of linear equations in two variables) class 10th mathematics are examples 1, 2, 4, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19.
How do NCERT Solutions for Class 10 Maths Chapter 3 help in exam preparation?
NCERT Assignments Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables are an essential tool for exam preparation. They provide detailed, step-by-step solutions for all problems in the chapter, making it easier for students to understand concepts and solve questions confidently. These solutions also include Class 10 Maths Chapter 3 solved problems and important questions, which are likely to appear in exams. Practicing these regularly improves accuracy and speed in solving linear equations. The solutions focus on developing problem-solving techniques, ensuring that students are well-prepared for both board exams and competitive tests.
Which chapter should recall before starting class 10th Math chapter 3?
Yes, before starting class 10th mathematics chapter 3 (Pair of linear equations in two variables), students should recall chapter 4 (Linear Equations in Two Variables) of class 9th mathematics.
Are NCERT Class 10 Maths Chapter 3 solutions available for free download?
Yes, many platforms offer NCERT Class 10 Maths Chapter 3 solutions PDF for free download. These PDFs contain comprehensive solutions to all exercises, enabling students to study offline at their convenience. Websites offering free downloads often include additional resources such as Class 10 Maths Chapter 3 practice questions and a solution guide. These resources are structured to help students grasp concepts more effectively and provide quick revision material before exams. The free availability of these solutions ensures that every student has access to high-quality learning materials, irrespective of financial constraints.
What are real life applications of class 10th Maths chapter 3?
Some real life applications of class 10th mathematics chapter 3 (Pair of linear equations in two variables) are:
To solve age related problems.
Example: Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
To solve speed, distance and time related problems.
Example: Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
To solve cost related problems.
Examples: The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, she buys 3 bats and 5 balls for Rs1750. Find the cost of each bat and each ball.
To solve geometry problems.
Example: In a ∆ABC, ∠ C = 3 ∠ B = 2 (∠A + ∠ B). Find the three angles.


