NCERT Solutions for Class 10 Maths Chapter 13 Exercise 13.3 Statistics in Hindi and English Medium for academic session 2025-26. The solutions of question given in Exercise 13.3 of 10th Maths are solved through Videos and Images. It helps the students to know the steps of solution of questions.
Class 10 Maths Exercise 13.3 Solutions
Class 10 Maths Exercise 13.3 in Hindi
Class 10 Maths NCERT Book Download
Class 10 Maths Chapter 13 Solutions
Class 10 Maths all Chapters Solutions
Class 10 all Subjects NCERT Solutions
Class 10 Maths Exercise 13.3 Solutions in Hindi and English Medium
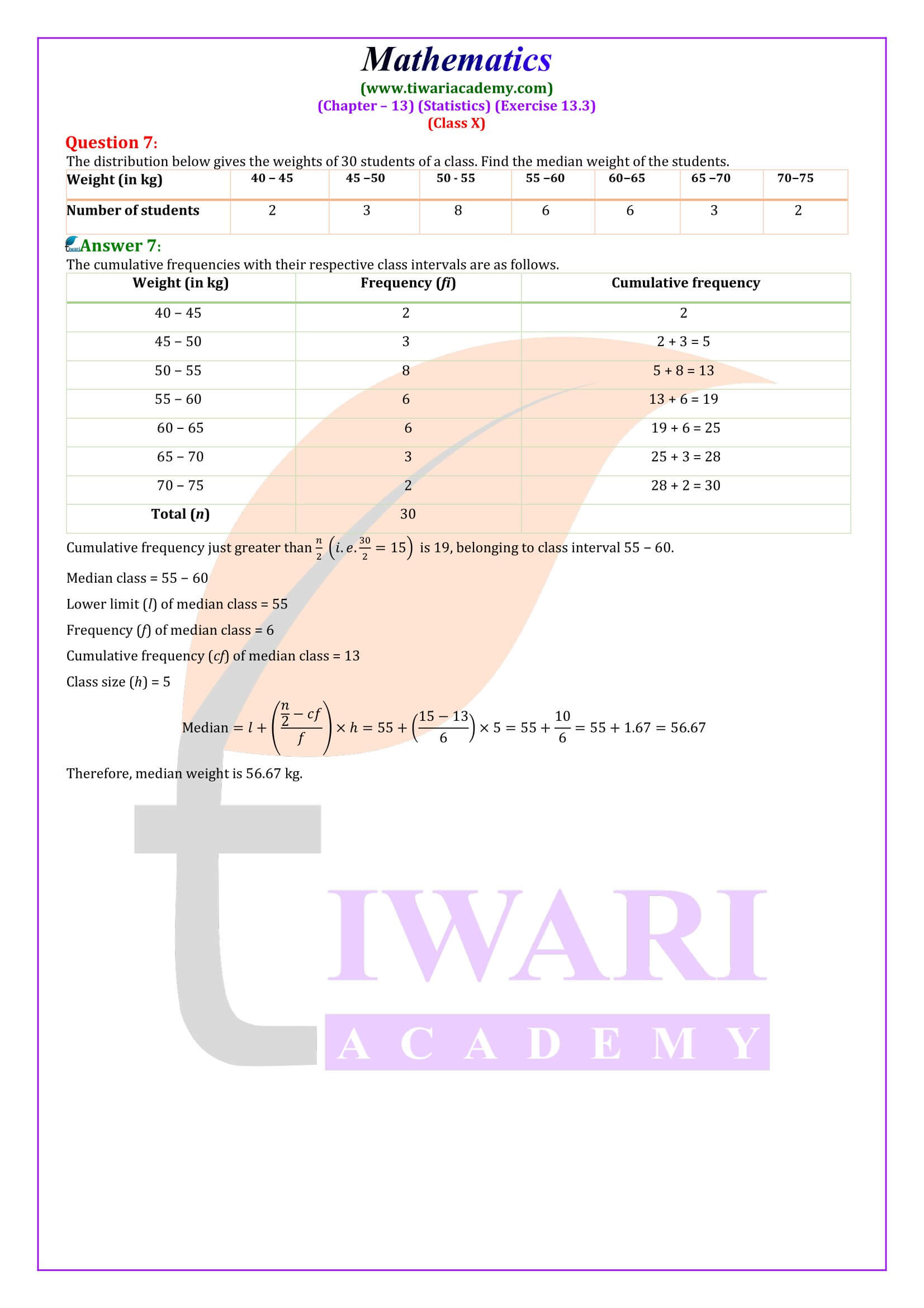
To prepare for questions on the median, focus on understanding how to locate the middle value of a dataset. For grouped data, identify the median class, which is the class whose cumulative frequency is closest to 𝑛/2, where 𝑛 is the total number of data points. The formula to find the median is Median = 𝑙 + (𝑛/2 − cf)/𝑓 × ℎ, where 𝑙 is the lower boundary of the median class, 𝑐f is the cumulative frequency of the class before the median class, 𝑓 is the frequency of the median class, and ℎ is the class width.
To master this topic, practice cumulative frequency distributions and learn how to interpret them. Practice problems will help you become adept at finding the cumulative frequency of classes and using the formula to calculate the median. As with other measures of central tendency, compare the median with the mean and mode in various scenarios. Practice a variety of problems so that you can quickly identify the median class and apply the formula accurately during exams.

| Class: 10 | Mathematics |
| Chapter: 13 | Statistics |
| Exercise: 13.3 | NCERT Solutions in PDF and Videos |
| Session: | CBSE 2025-26 |
| Medium: | English and Hindi medium |
NCERT Books based solutions are available in Hindi and English Medium for all the students of CBSE Board, UP Board, MP Board and all other board who are using NCERT Textbooks for their exams. Practice with videos solutions as well as PDF solutions for the preparation of school tests and terminal exams.
Median of Grouped Data
We have already studied in previous classes; The mean is a measure of central tendency that gives the value of the most intermediate observations in the data. To find the median of arbitrary data, we first arrange the data values of observations in ascending otherwise descending order. So if n is odd, the median is observation of (n + 1) / 2. And, if n is even, the median will be the average of (n / 2) th and (n / 2 + 1) th observations. In class 10, we will find the mean of the frequency distribution. We will add another column that represents all the information for the frequency table and as a cumulative frequency column.
The best suited Measure of Central Tendency
The mean is the most commonly used measure of central tendency because it takes into account all observations and falls between extremes, that is, the largest and smallest observations in all data. It also helps with the comparison of two or more distributions. For example, by comparing the average (average) results of students from different schools in a particular exam, we can conclude which school performs better.
However, too large or too small values in the data affect the mean. For example, the mean of classes that have nearly identical frequencies is a good representative of the data. But, if one class has a frequency, say 2, and the other five have a frequency of 20, 25, 20, 21, 18, then the mean will certainly not reflect how the data behaves. For this type of cases, the mean is not so useful for the representation of data.
Median through a Specific Observation
In problems where individual observations are not important, and we want to get a ‘specific’ observation, the median is more appropriate, for example, the specific productivity rate of workers, the average wage in a country, etc. Price can be. Therefore, instead of the mean, we take the mean as a better measure of central tendency.
In situations that require the most value or the most popular item set, the mode is the best option, for example, to watch the most popular television programs, the most in-demand consumer item, vehicle color used by most users. is done. People etc.
Empirical Formula between Mean, Mode and Median
The Empirical Relationship between the three measures of central tendency:
3 Median = Mode + 2 Mean
In which cases in 13.3 of 10th Maths finding median is more appropriate?
In problems where individual observations are not important, and we wish to find out a ‘typical’ observation, the median is more appropriate, e.g., finding the typical productivity rate of workers, average wage in a country, etc. These are situations where extreme values may be there. So, rather than the mean, we take the median as a better measure of central tendency.
Which questions or examples are important in 13.3 of 10th Maths?
In exercise 13.3 of class 10 math, there are 7 questions and two examples (examples 7, 8). All questions and examples of this exercise are important from the exam point of view.
How much time is needed to complete exercise 13.3 of class 10th mathematics?
Students need a maximum of three days to complete exercise 13.3 (chapter 13) of class 10th mathematics if they give 1-2 hours per day to this exercise. This time also depends on student’s speed, efficiency, capability and many other factors.
What will students learn in exercise 13.3 of class 10 Maths?
In exercise 13.3 of class 10 math, students will learn how to find Median of Grouped Data. This exercise is easy but needs practice to avoid calculation mistakes.