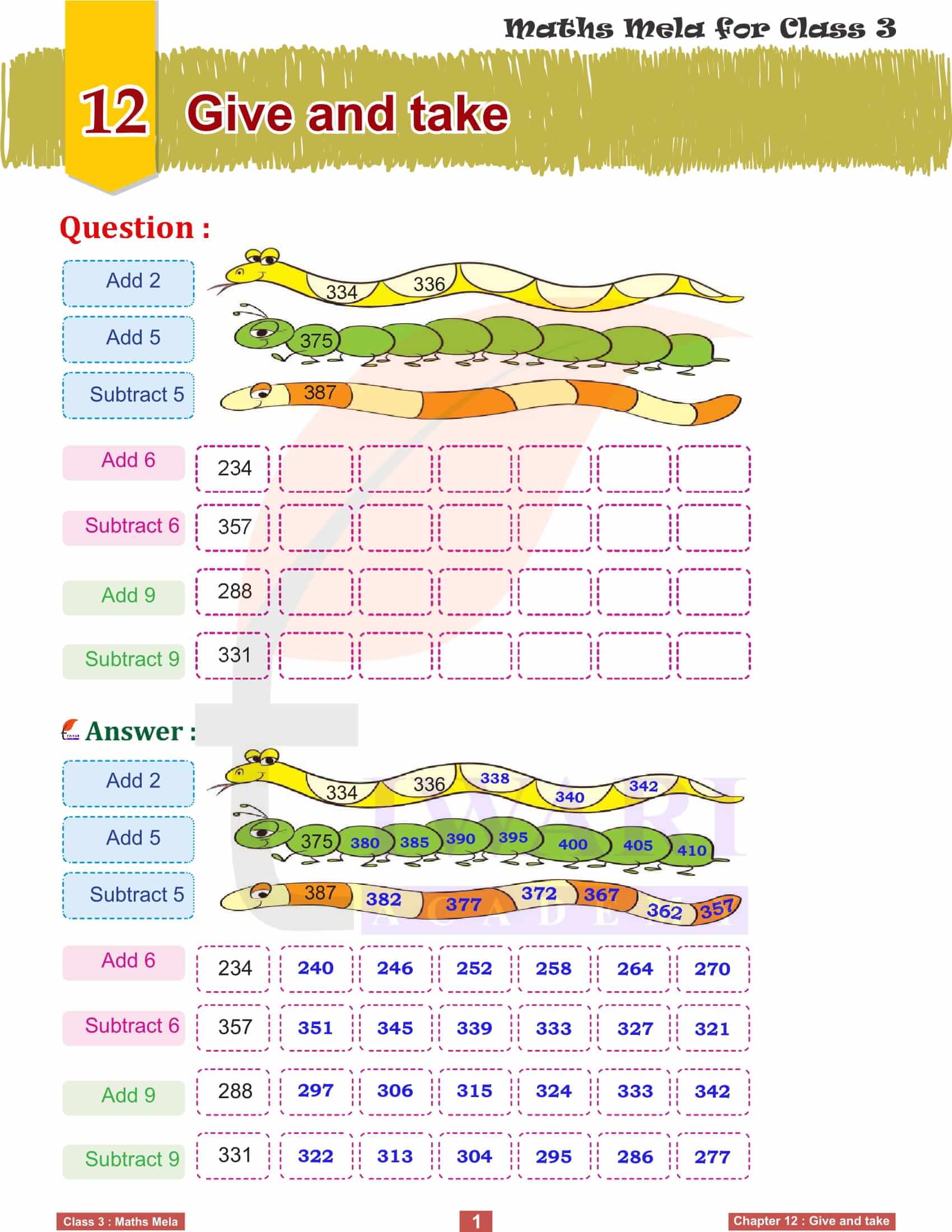
NCERT Solutions for Class 3 Maths Mela Chapter 12 Give and Take

Hello students! here, we will delve into Chapter 12 of our Maths book, Give and Take. This chapter focuses on the fundamental concepts of addition and subtraction. We will explore different strategies to add and subtract numbers, understand the importance of these operations in everyday life, and solve practical problems using these skills. Let’s start our journey by understanding the basic principles and significance of these mathematical operations.

Practical Examples of Addition
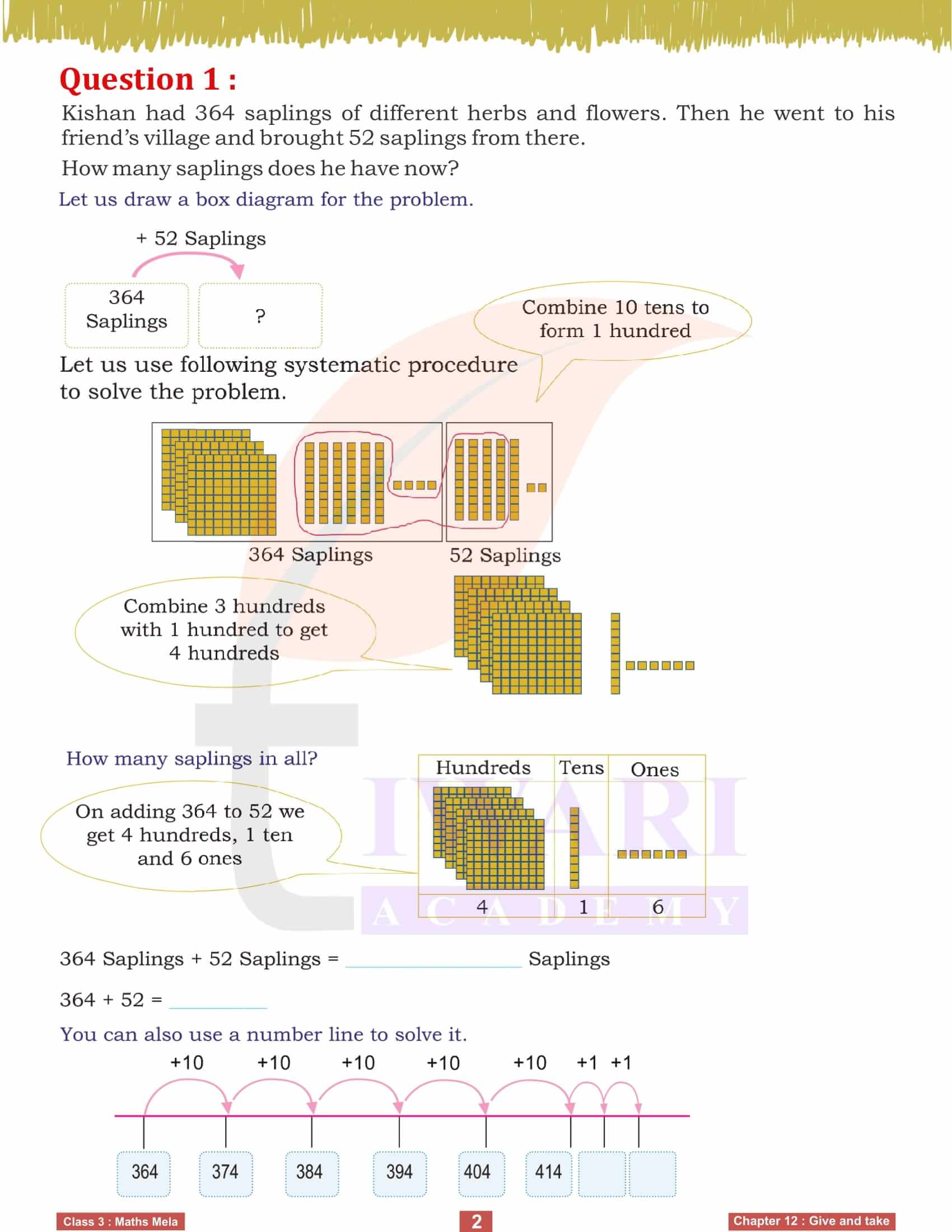
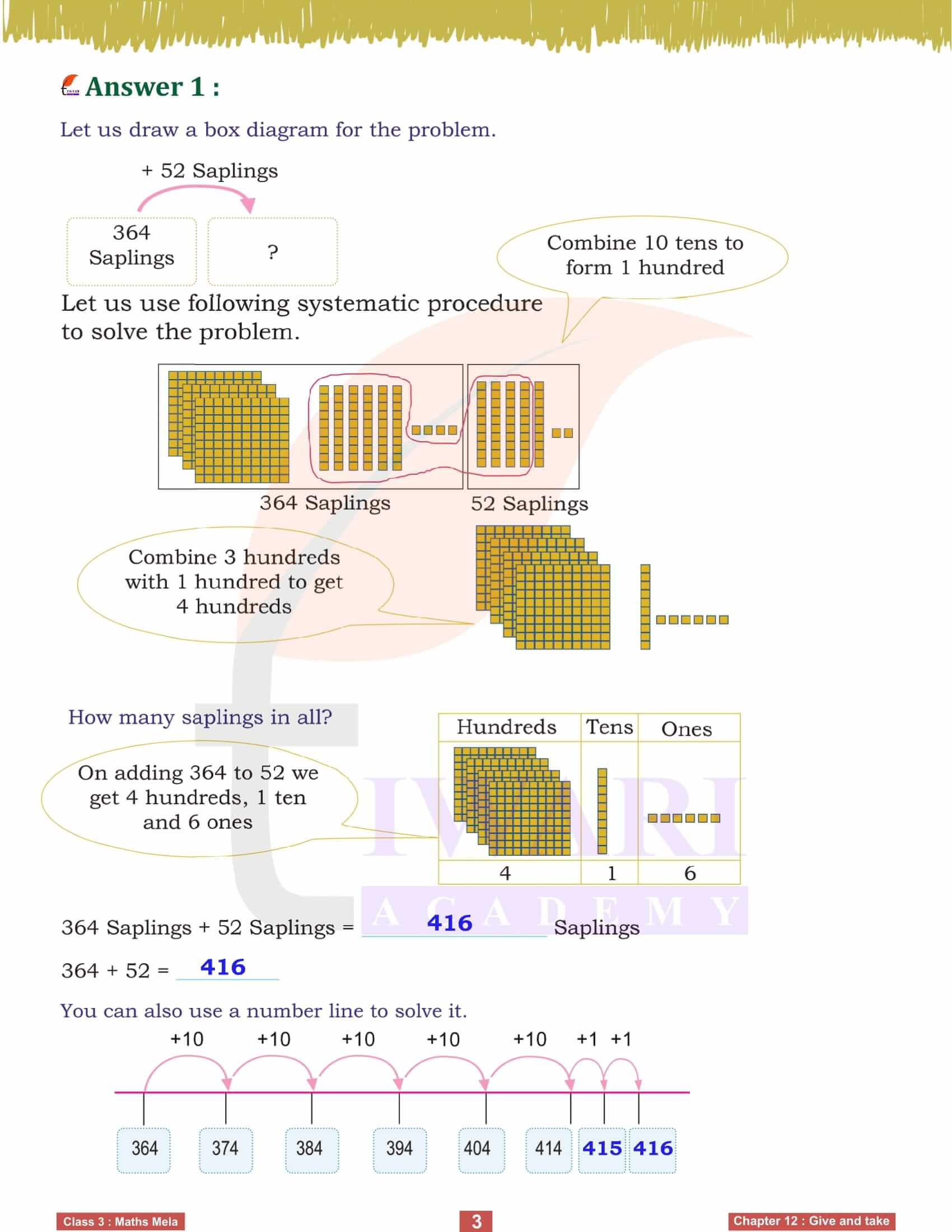
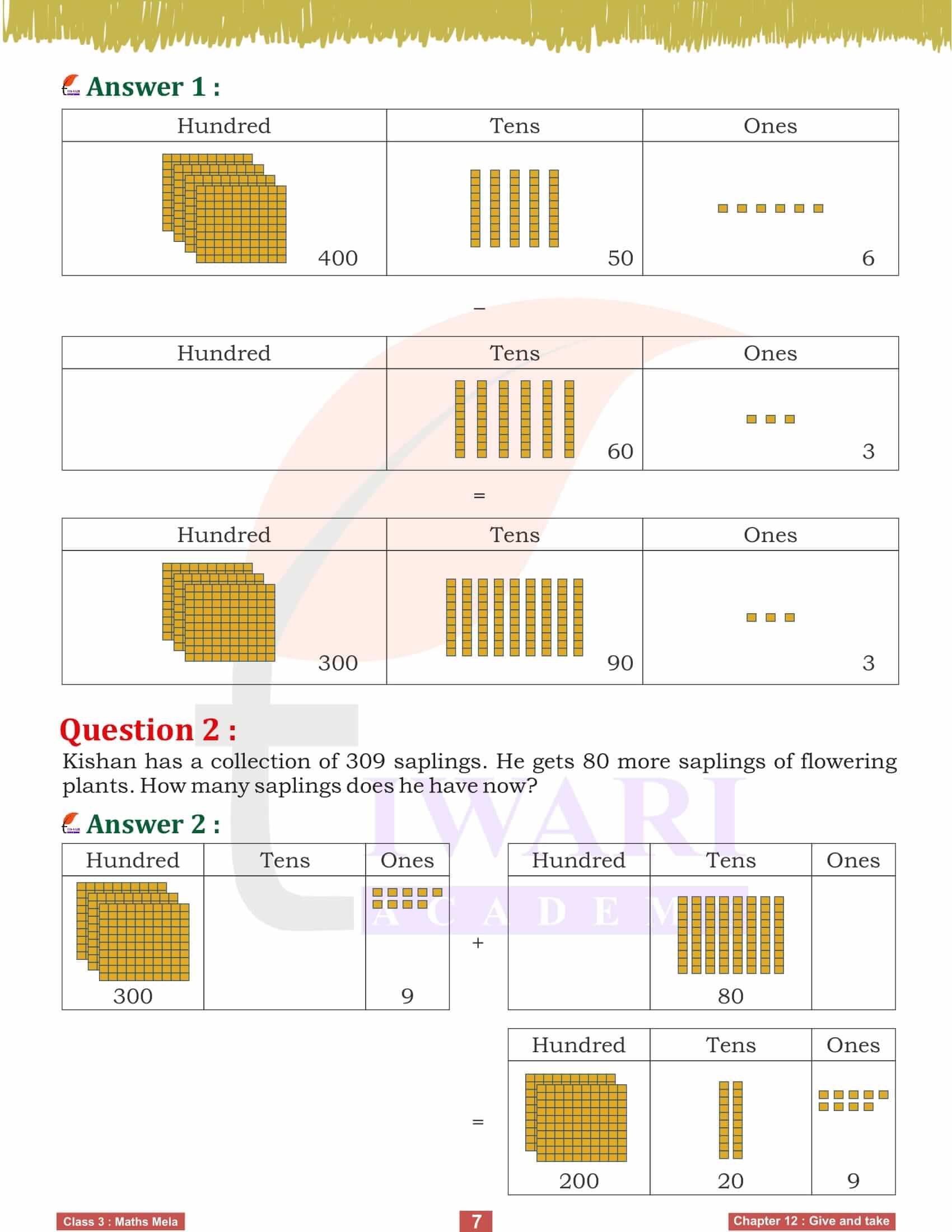
One of the primary examples in this chapter is about Kishan, who runs a plant nursery. He initially has 364 saplings and brings 52 more from a friend’s village. To find out how many saplings he has now, we simply add the two numbers: 364 + 52. This exercise not only teaches us how to perform addition but also emphasizes the importance of addition in real-life situations. By using a box diagram and systematic procedure, we can visualize and solve the problem effectively, ensuring a clear understanding of the concept.

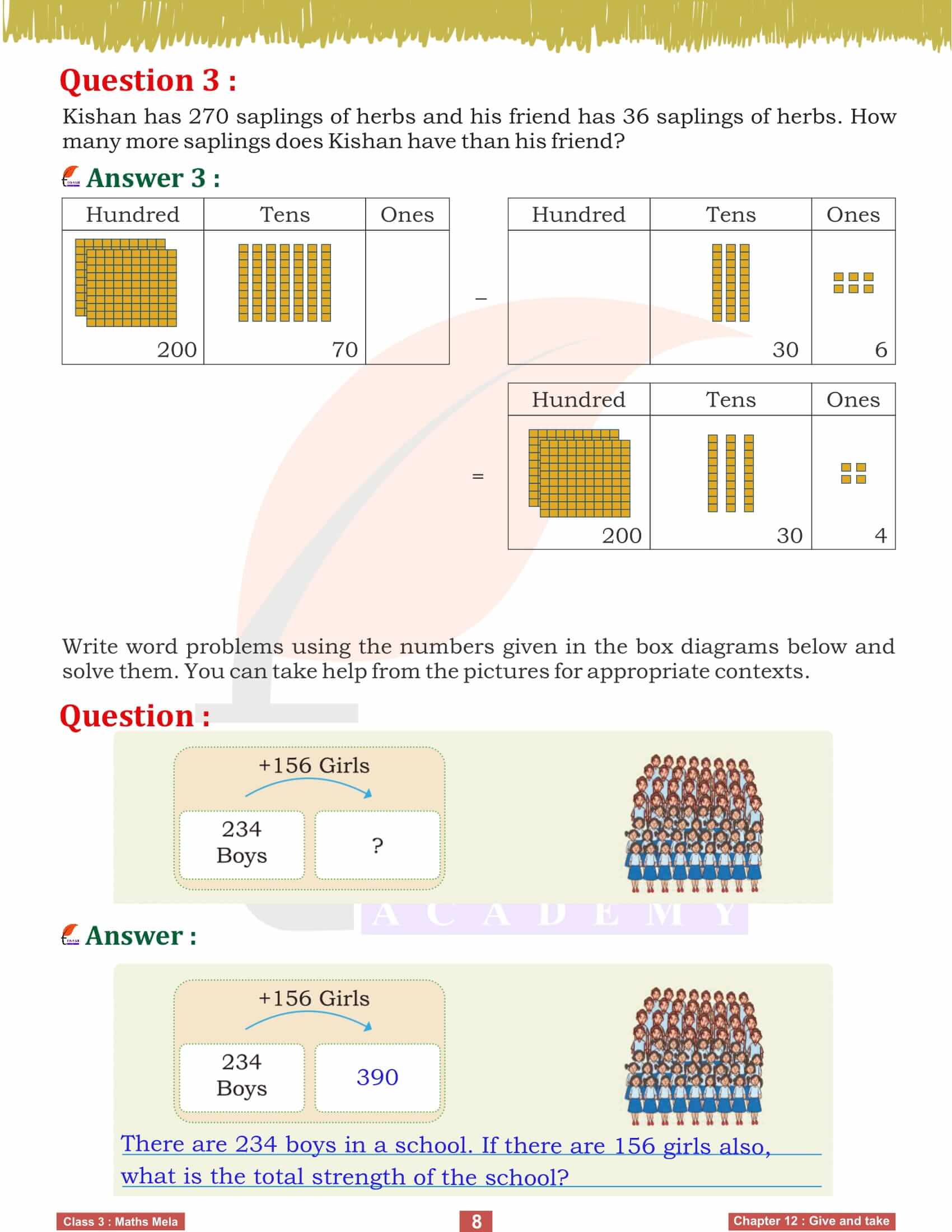
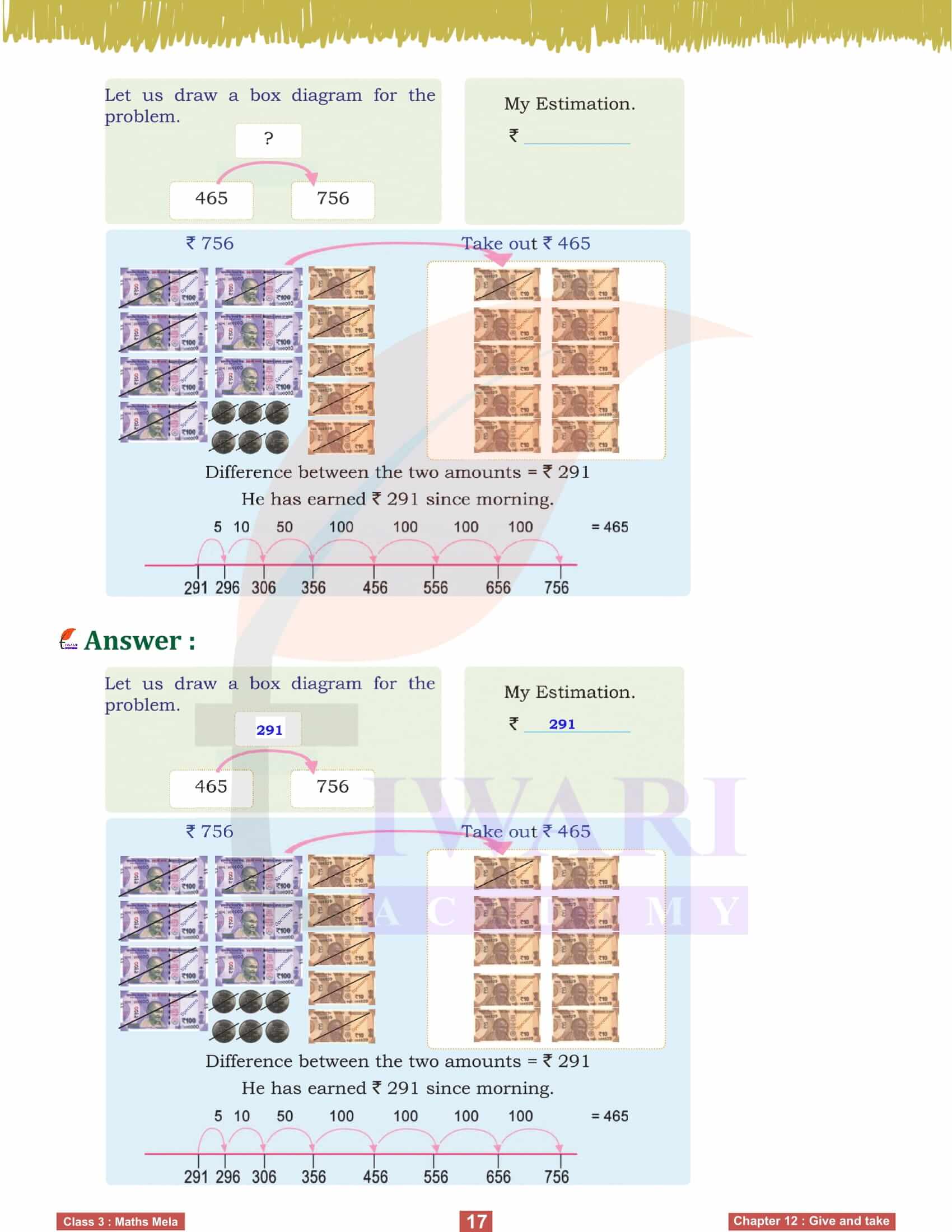
Subtraction is equally crucial, and Kishan’s example helps us understand this. He needs to deliver 230 saplings to a school and has already packed 75. To find out how many more saplings he needs to pack, we subtract 75 from 230. Using number lines and block diagrams, we can break down the problem into simpler steps, making it easier to solve. This methodical approach helps us grasp the subtraction process and its practical applications in daily activities.

Using Dienes Blocks and Number Lines
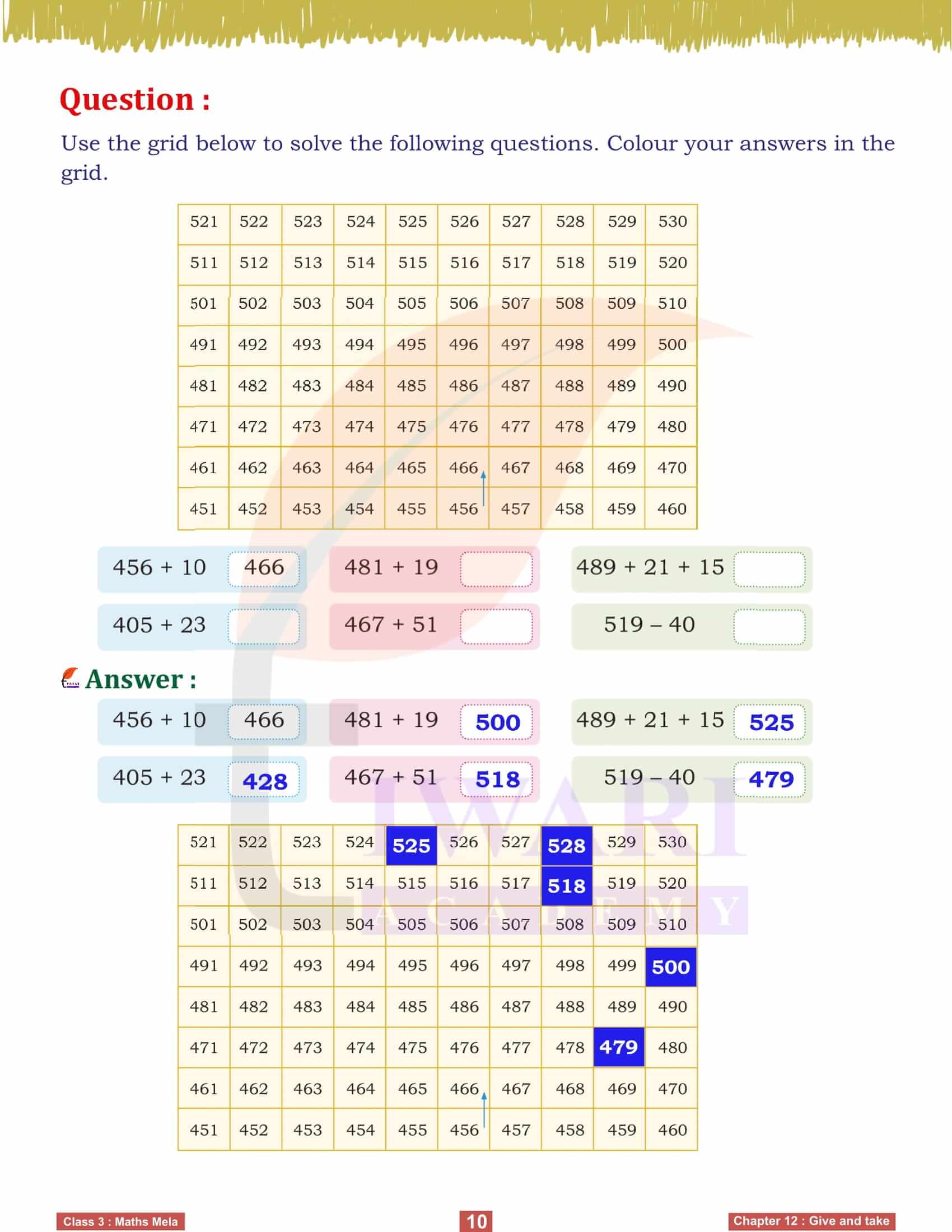
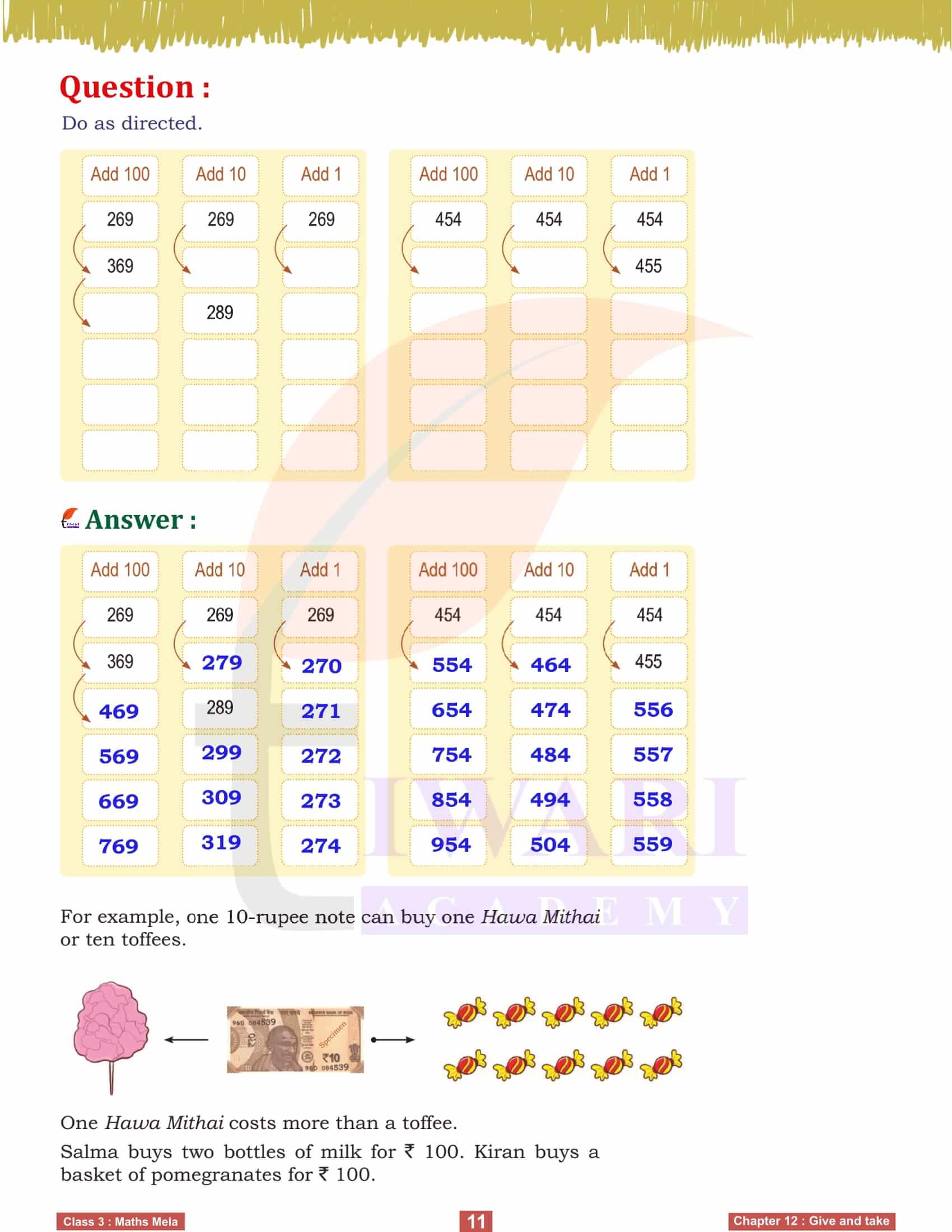
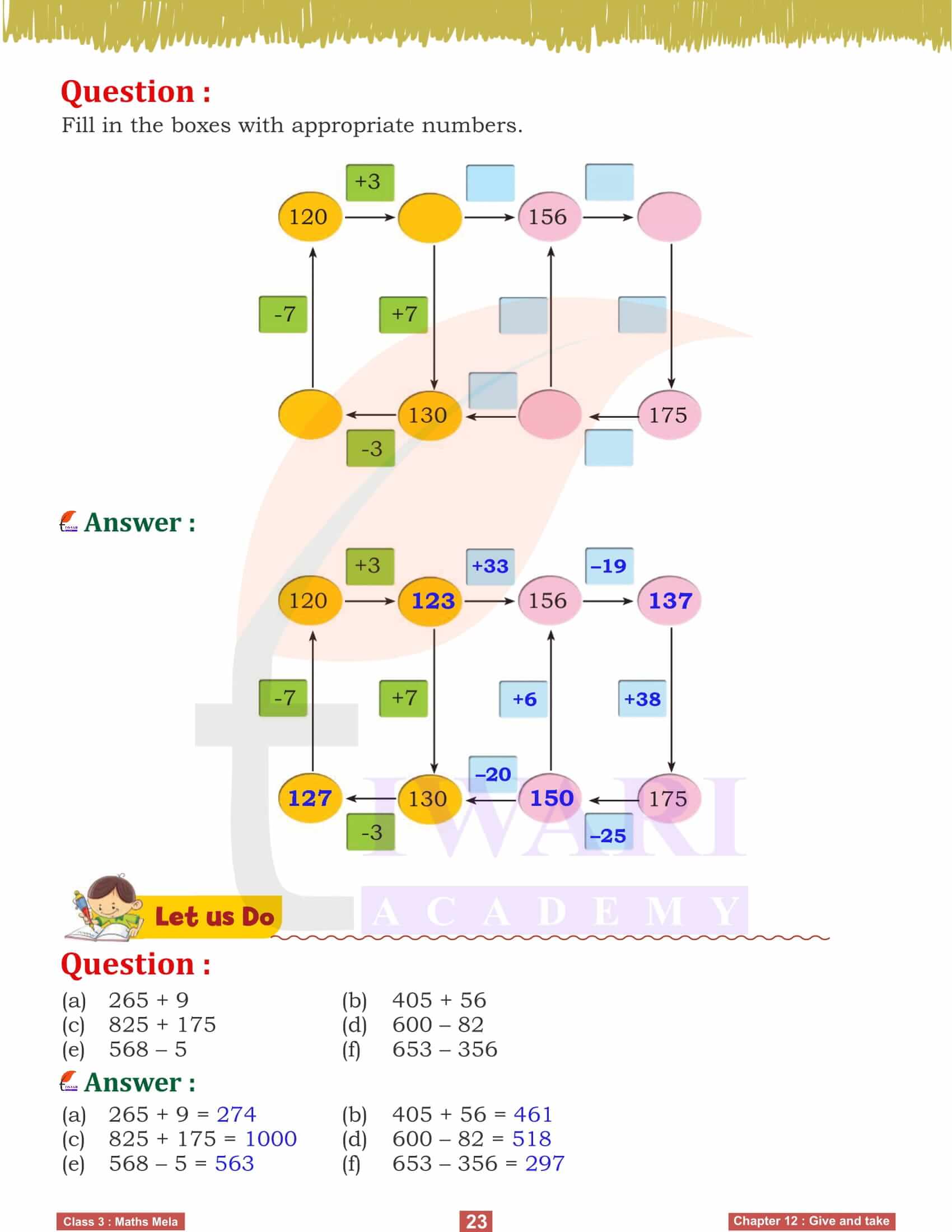
To make addition and subtraction more tangible, we use tools like Dienes blocks and number lines. These visual aids help us comprehend the relationship between hundreds, tens, and ones, making it easier to perform these operations. For instance, converting tens into hundreds or ones when necessary simplifies complex problems, ensuring we understand the mechanics behind the numbers. By practicing with these tools, we enhance our problem-solving skills and mathematical fluency.

The chapter 12 also introduces the concept of exchanging goods, reminiscent of the old barter system. We learn how different quantities were exchanged based on need and value. This analogy helps us understand the concept of value and comparison, crucial for making informed decisions in addition and subtraction. We also explore modern currency, understanding how different denominations can be used to purchase goods, further cementing our understanding of these mathematical operations.

Word Problems and Estimation
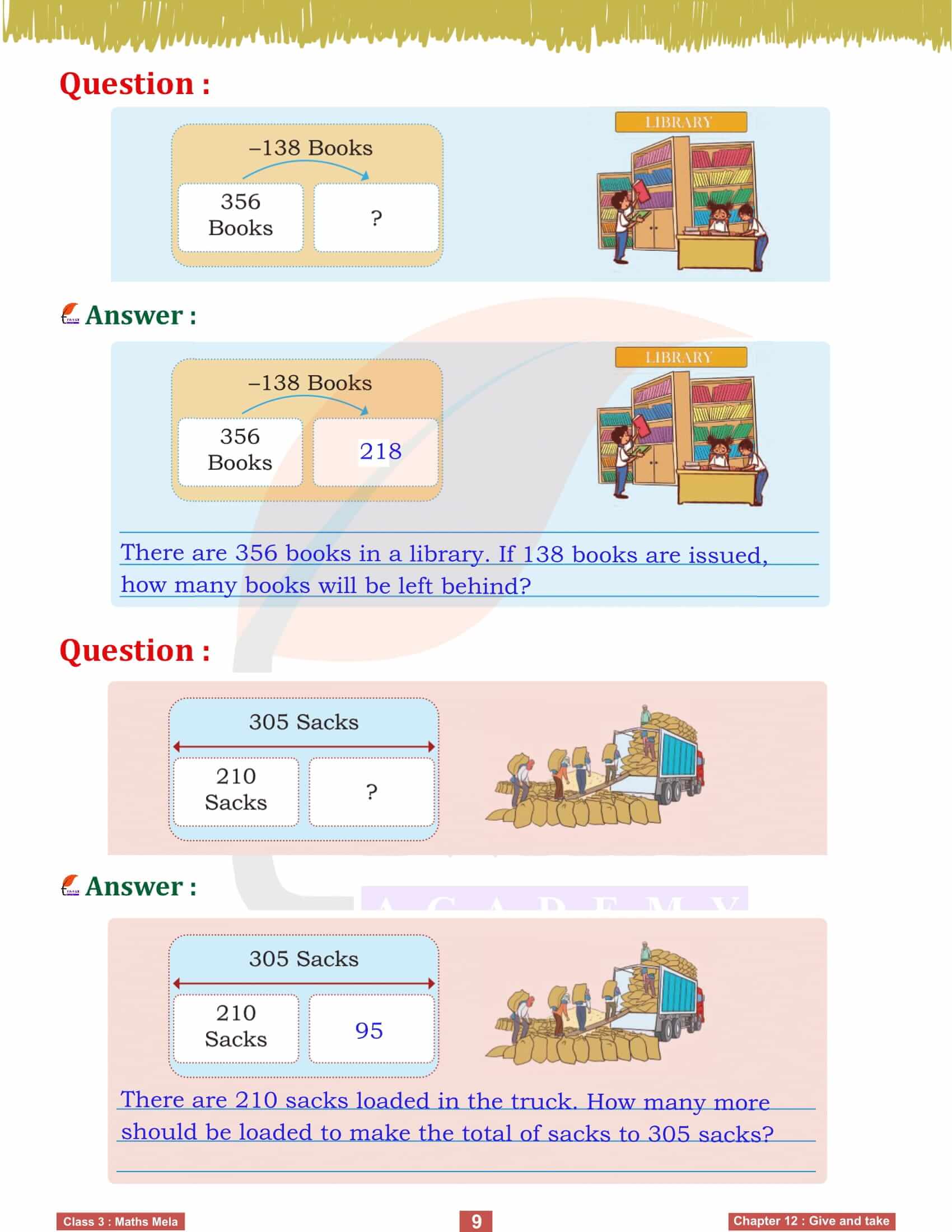
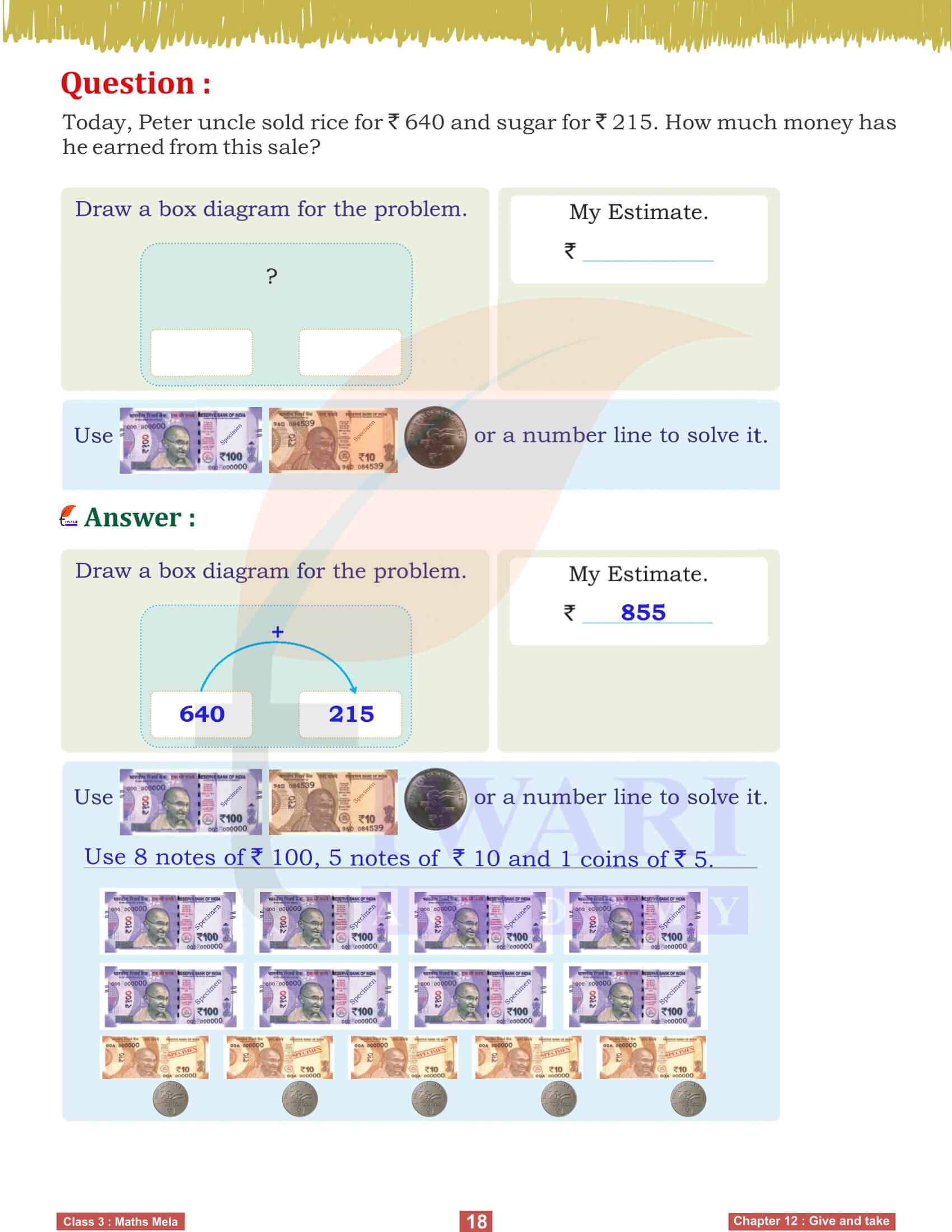
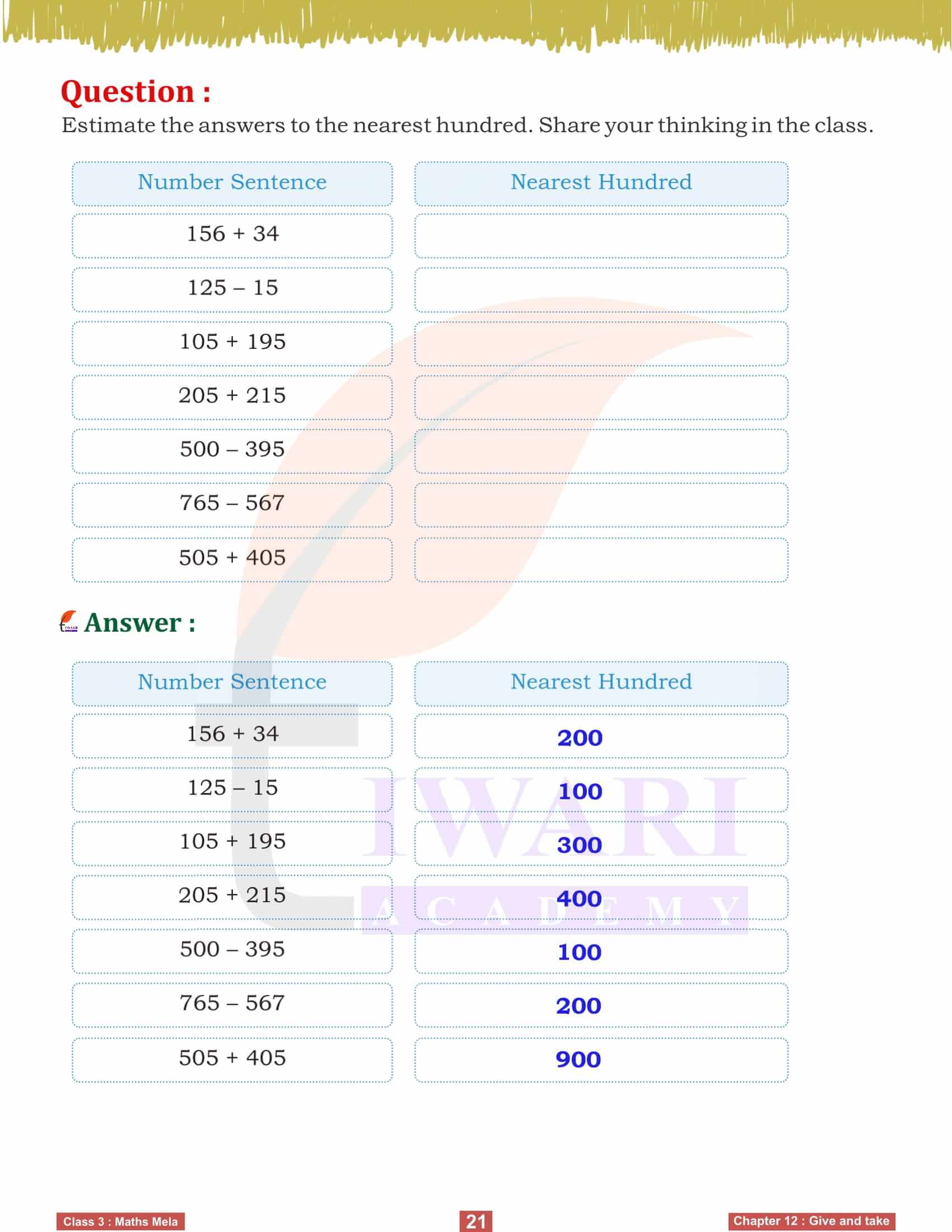
Word problems play a significant role in this chapter, helping us apply addition and subtraction in various contexts. For example, calculating how many saplings are left after distributing some or how much money is earned from sales involves these operations. By solving these problems, we learn to frame mathematical equations based on real-life scenarios, enhancing our analytical skills. Estimation techniques also help us make quick and reasonable guesses, improving our ability to solve problems efficiently.

In conclusion, Chapter 12 “Give and Take” equips us with essential skills in addition and subtraction, using practical examples and visual aids. By understanding and practicing these concepts, we become proficient in handling numbers, preparing us for more advanced mathematical challenges. Keep practicing with the provided exercises and use the strategies discussed to solve various problems. Remember, the key to mastering Maths is consistent practice and understanding the underlying principles.